例題はこちら(画像をクリックするとPDFファイルで開きます。)
\(x \gt 0\) , \(y \gt 0\) のとき相加平均と相乗平均の関係
\(\displaystyle \frac{x+y}{2} \geq \sqrt{xy}\)
は基本中の基本ですが、この相加平均と相乗平均の誤差について考えていく問題です。
結論が示されている証明形式であるため、問題を解くこと自体は標準的な難易度です。
まずは例題でウォーミングアップをして、同じテーマを扱ってはいますがより手ごわい類題にもチャレンジしてみてください。
類題はこちら(画像をクリックするとPDFファイルで開きます。)
特に (2) , (3) は評価が下手だと不等式証明に失敗しかねません。
誘導を使うにしても
一度研いで切れ味をよくしてから使う
という態度が必要です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 左側の不等式は相加平均・相乗平均の関係そのものです。 右側の不等式も手なりに差を取れば問題ないでしょう。 $$\begin{eqnarray} と、\(\sqrt{x}\) で括れば、条件 \( 0 \lt x \lt y\) という条件から \(\sqrt{x}(\sqrt{y}-\sqrt{x}) \gt 0\) が言え、証明完了です。 漸化式 $$\begin{eqnarray} という漸化式があるため、証明の手法としては 数学的帰納法 の一択と言ってよいでしょう。 例題の不等式の結果、及びはさみうちの原理から \(\displaystyle \lim_{n \to \infty} (y_{n}-x_{n})=0\) ということが言えます。 この数列 \(\{x_{n}\}\) , \(\{y_{n}\}\) のイメージを数直線上に図示すると のように、 段々と両サイドから挟まれていく感じのイメージとなります。 そりゃ、\(\displaystyle \lim_{n \to \infty}x_{n}=\displaystyle \lim_{n \to \infty}y_{n}\) になるわ という気持ちになるでしょう。 問題はこちら(画像をクリックするとPDFファイルで開きます。) \(a_{n+1}=\displaystyle \frac{a_{n}+b_{n}}{2}\) , \(b ... 続きを見る なども参考にしてみてください。 類題も例題同様、相加平均と相乗平均の差についてを考えていくわけですが、オチの不等式はかなり絶妙に数値設定してあります。 上で述べた、数直線上のイメージがあると、「そりゃそうだ」と言える内容です。 もちろん、数式的にキッチリしめすとなると数学的帰納法です。 $$\begin{eqnarray} と手なりに差を取り \(b_{n} \geq a_{n}\) であることを用いて、「小さくしよう」という気持ちで評価すると $$\begin{eqnarray} となり、失敗します。 ここからのリカバリーをどうするかが頭の使いどころです。 \(X_{n+1} \leq r X_{n}\) というような、 番号を下げて、上から押さえる という形で評価することは難関大受験生であれば割とお馴染みの形です。 お馴染みでなかったら 問題はこちら(画像をクリックするとPDFファイルで開きます。) 縮小関数による漸化式の極限という、難関大ではちょこちょこ出題されるテーマです。 もし、初見であれば、まずは初見でやってみて ... 続きを見る などを参考にしてお馴染みにしてください。 今回の不等式を見て 「2乗?」 と思えたら逆にそれが突破口です。 \(b_{n+1}-a_{n+1}=\displaystyle \frac{(\sqrt{b_{n}}-\sqrt{a_{n}})^{2}}{2}\) なのですが、分子の有理化をすると \(b_{n+1}-a_{n+1}=\displaystyle \frac{(b_{n}-a_{n})^{2}}{2 (\sqrt{b_{n}}+\sqrt{a_{n}})^{2}}\) ということになり、\((b_{n}-a_{n})^{2}\) というパーツが登場します。 あとは分母を見て \((\sqrt{b_{n}}+\sqrt{a_{n}})^{2} \geq 4a_{n}\) となる根拠を探せばよく、それを示すことで \( \leq \displaystyle \frac{ \ }{8a_{n}}\) という形で上から押さえることができます。 \(b_{1}-a_{1} \geq b_{2}-a_{2} \geq \cdots \) と、誤差がどんどん小さくなっていくのは (1) の不等式から当然で、どの段階で誤差が \(4\) 未満になるかが問われています。 $$\begin{eqnarray} $$\begin{eqnarray} $$\begin{eqnarray} と実験も、この辺りが限界でしょう。 (1) や (2) の不等式をどのように活用するかが勝負の分かれ目です。例題について
例題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
(1) について
\displaystyle \frac{y-x}{2}-(\displaystyle \frac{x+y}{2}-\sqrt{xy})&=& \sqrt{xy}-x \\
&=&\sqrt{x}(\sqrt{y}-\sqrt{x})
\end{eqnarray}$$(2) について
\left\{
\begin{array}{l}
x_{n} =\sqrt{x_{n-1}y_{n-1}} \\
y_{n} = \displaystyle \frac{x_{n-1}+y_{n-1}}{2}
\end{array}
\right.
\end{eqnarray}$$この数列のイメージ
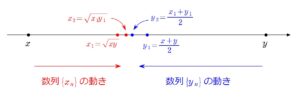

参考算術幾何平均【漸化式で定まる数列の極限】【2010年度 北海道大学】
類題について
類題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
(1) について
(2) について
\displaystyle \frac{1}{8a_{n}}(b_{n}-a_{n})^{2}-(b_{n+1}-a_{n+1}) &=& \displaystyle \frac{1}{8a_{n}}(b_{n}-a_{n})^{2}-(\displaystyle \frac{a_{n}+b_{n}}{2}-\sqrt{a_{n}b_{n}}) \\
&=& \displaystyle \frac{{b_{n}}^{2}-6a_{n}b_{n}-3{a_{n}}^{2}+8a_{n}\sqrt{a_{n}b_{n}}}{8a_{n}}
\end{eqnarray}$$
\displaystyle \frac{{b_{n}}^{2}-6a_{n}b_{n}-3{a_{n}}^{2}+8a_{n}\sqrt{a_{n}b_{n}}}{8a_{n}} & \geq & \displaystyle \frac{{a_{n}}^{2}-6a_{n}b_{n}-3{a_{n}}^{2}+8a_{n}\sqrt{a_{n}a_{n}}}{8a_{n}} \\
&=& \displaystyle \frac{6{a_{n}}^{2}-6a_{n}b_{n}}{8a_{n}}\\
&=& \displaystyle \frac{6a_{n}(a_{n}-b_{n})}{8a_{n}}\\
& \leq & 0
\end{eqnarray}$$

参考縮小関数による漸化式の極限【関数によって定まる数列の極限】【1994年度 筑波大学】
(3) について
\left\{
\begin{array}{l}
a_{1}= 100 \\
b_{1}= 900
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
a_{2}= 300 \\
b_{2}= 500
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
a_{3}= 100\sqrt{15} \\
b_{3}= 400
\end{array}
\right.
\end{eqnarray}$$


