問題はこちら(画像をクリックするとPDFファイルで開きます。)
通常の空間座標における回転体の体積自体、東大は好んで出題する傾向にありますが、本問は
180°しか回転しない回転体の体積
について扱います。
このような「こうなったらどうする?」という味付けは教育的で、いかにも東大らしい良問だと思います。
とは言え、難易度という点では少しハードかなとは思います。
初見の方はぜひ考えてみてください。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む のようなイメージで 180 ° 回転します。 このあとは、回転軸である \(y\) 軸に垂直に切った断面図を捉えます。 空間座標における回転体の体積を考える処方箋 空間座標における回転体の扱い方 という考え方の中でも、 「切ってから回す」 という態度で考えます。 \(y=k\) で切った切り口のうち、\(x \geq 0\) という範囲にある部分を考えると という断面となります。 これについては半円の差を考えれば解決するようなものです。 今度は 180°しか回転しないということが、もろに牙をむきます。 断面は の打点部分です。 これを直接出すのは億劫です。 さらに、求められているものが\(V(a)\) そのものではなく、\(\displaystyle \lim_{a \to \infty} V(a)\) であることも後押ししますので、等式を諦め、不等式を繋ぐことで、最終的な目標である極限を「はさみうちの原理」で仕留めるという構想を立てていきます。 そこで と長方形で囲んでしまって評価する路線を考えたいと思います。 ここまでが、実際に脳みそを使う部分で、この後は、実際のところ計算勝負ということになります。 その際、考え方によっては事故がおこるような答案が出ても不思議ではないような落とし穴があります。 それについては【総括】で触れておきました。 色々な空間座標の回転体について場数を踏みたい方は以下もご活用ください。 空間座標における回転体の体積【円錐の回転体の体積とその工夫】【2017年度 東京大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) (1) は難関大志望者であれば、特に手が止まることはないでしょう。 点 \(P\) の軌跡が円となることも容易に把握できると思います。 問題は (2) です。 点 \(Q\) が \(OQ=1\) を満たしながら、平面 \(x=0\) を動くということは, 点 \(Q\) は原点 \(O\) を中心として平面 \(x=0\) で回転しています。 線分 \(OP\) とはいわば円錐の「母線」です。 点 \(Q\) の回転に伴って ... 空間座標における回転体【ズレて刺さった団子の回転体】【2014年度 名古屋大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 空間座標における回転体というトピックスで、難関大を目指すにあたっては避けては通れない話題です。 一般に 空間座標における回転体の扱い方 全体像を捨てろ 切ってから回す(先に回すな) 回転の中心からの最大距離・最小距離を捉える がポイントになる点です。 全体像については「仮に分かったとしても、それが体積を求めることに役に立つのか?」ということを考えれば、考えるだけ無駄です。 むしろ混乱するだけなので、考えない方がいいぐらいです。 ... 空間座標における回転体【ベビースターラーメンの回転体】【2003年度 東北大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 空間座標における回転体は出題されれば差が付くトピックスです。 難関大を目指すにあたってはしっかりと準備しておきたい話題ですので、しっかりとマスターして周りの受験生に差をつけましょう。 一般に 空間座標における回転体の扱い方 全体像を捨てろ 切ってから回す(先に回すな) 回転の中心からの最大距離・最小距離を捉える がポイントになる点です。 全体像については「仮に分かったとしても、それが体積を求めることに役に立つのか?」ということを ... 仮想難関大(オリジナル予想問題)【微積分~空間座標における回転体】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 仮想難関大シリーズということで、東大、京大をはじめとする旧帝大、東工大、国公立大学医学部医学科などの難関国公立大を想定したオリジナルの自作問題です。 「手垢の付いていない問題で最後の力試しがしたい」 という方はぜひご活用ください。 本問は最初は \(z\) 軸回転として作ろうと思っていましたが、よくよく考えると \(z\) 軸回転だと円錐 ということになり、問題としては面白くなかったので、\(y\) 軸回転体にしま ... イメージ図について
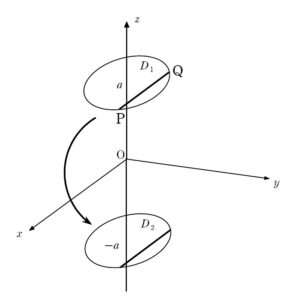
(1) について
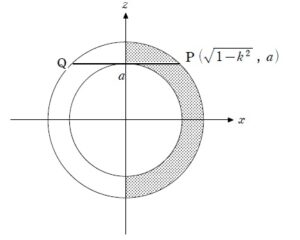
(2) について
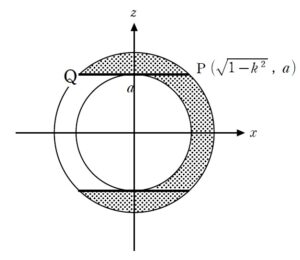
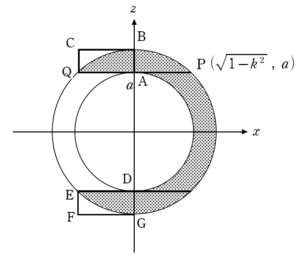
その他の空間座標における回転体の体積について





