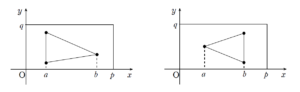例題はこちら(画像をクリックするとPDFファイルで開きます。)

類題はこちら(画像をクリックするとPDFファイルで開きます。)

類題2はこちら(画像をクリックするとPDFファイルで開きます。)

内包関係にある三角形と長方形の面積に関する論証問題で、ある意味「そりゃそうだろ」的な主張です。
ただ、こういった論証問題の場合どこまで掘り下げて示せばよいのかが難しいものです。
加えて、配置が自由であるため
「あんたが描いた絵だったらいいかもしれないけど、こういうケースはどうすんの?」
的な突っ込みに耐えられるかどうかという不安がつきまといます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
例題について
例題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

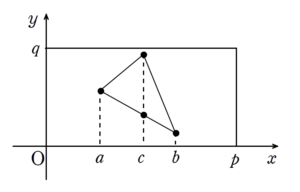
座標で考えてみます。
座標で考えなくとも、同じような考え方はできますが、数式化しやすいので。

のように
というシチュエーションが一般的です。
ただ、

というような
というケースもありえます。
\(a \leq c \leq b\)
というように等号を入れた不等号を用いて一気に処理することも可能ですが、【解1】では場合分けして処理しました。
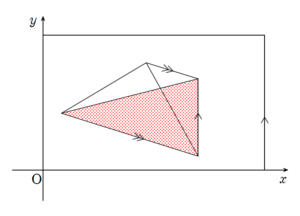
等積変形を用いると
場合分けしてもよいですが、結局は

という
となるケースは

というように平行線を引くことで、
のケースに帰着でき、そのような路線で解答をまとめることもできるでしょう。
ただ、
- 長方形の枠をはみ出さずに平行線を引いて等積変形できるかどうか
ということについて、不備なく論じきるとなると、また神経をすり減らします。
それをまとめきれる自信があれば全然かまいませんが、実際その労力があれば、上述のように素直に場合分けして処理してしまった方が早いでしょう。
この路線でまとめるのであれば、後述の類題2を参考にしてみてください。
類題について
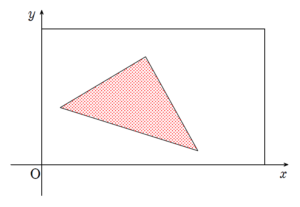
類題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

今度は三角形の中に内包される長方形の面積を考えます。
外と内が違うだけですが、勝手が違うものがあります。
類題2について
類題2はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

例題の長方形を平行四辺形とした場合です。
例題で等積変形でまとめることが大変だと述べましたが、(1) の
だということが保証されれば、等積変形でまとめあげることもできます。
例題の解答はコチラ
類題の解答はコチラ
類題2の解答はコチラ