アステロイドの射影【ベクトル方程式の活用】【1999年度 お茶の水女子大学】

イメージ図

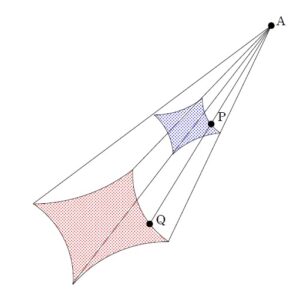
ひとまずは問題の図形 $D$ ,  $D'$ のイメージを掴みたいと思います。

図形 $D$ の境界線が表す曲線を $C$ ,  図形 $D'$ の境界線が表す曲線を $C'$ とします。

$C$ は平面 $z=1$ 上のアステロイドであり、$C$ 上の 1 点 $\mathrm{P}$ に光が当たったときを考えてみます。

すると

というようなイメージで $\mathrm{Q}$ が対応します。

点 $\mathrm{P}$ が $C$ 上を動いたときの $\mathrm{Q}$ の軌跡が $C'$ ということに他なりません。

$\mathrm{P}$$(x \ , \ y \ , \ 1)$ ,  に対して、$\mathrm{Q}$$(X \ , \ Y \ , \ 0)$ が対応したとすると、目標とすべきことは $X$ ,  $Y$ の関係式を Get することです。

$\overrightarrow{\mathrm{AQ}}=t\overrightarrow{\mathrm{AP}}$

と、$\overrightarrow{\mathrm{AP}}$ を伸ばして $\overrightarrow{\mathrm{AQ}}$ を得るという方向性を考えることになります。

この $t$ は、点 $\mathrm{Q}$ が平面 $z=0$ 上に乗るような

うまい倍率 $t$

という意識が大切です。

$$\begin{eqnarray} \overrightarrow{\mathrm{OQ}}&=& \overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{AP}} \\ &=& (1-t)\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OP}} \end{eqnarray}$$

ですから、$\overrightarrow{\mathrm{OQ}}$ を成分で表すと

$$\overrightarrow{\mathrm{OQ}}=\left( \begin{array}{c} (x-a)t+a \\ (y-b)t+b\\ (1-h)t+h \end{array} \right)$$

ということになります。

$z$ 成分が $0$ となることから、

$(1-h)t+h=0$

すなわち

$t=\displaystyle \frac{h}{h-1}$

と $t$ が求まります。

これにより、

$$\begin{eqnarray} \left\{ \begin{array}{l} X=\displaystyle \frac{h}{h-1} \cos^{3}{\theta}-\displaystyle \frac{1}{h-1}a\\ Y=\displaystyle \frac{h}{h-1} \sin^{3}{\theta}-\displaystyle \frac{1}{h-1}b \end{array} \right. \end{eqnarray}$$

と、$\mathrm{Q}$$(X \ , \ Y \ , \ 0)$ の軌跡が表す曲線 $C'$ のパラメータ表示が得られました。

あとは曲線の長さを得る公式

$\displaystyle \int_{\alpha}^{\beta} \sqrt{(\displaystyle \frac{dX}{d\theta})^{2}+(\displaystyle \frac{dY}{d\theta})^{2}} d\theta$

を用いて捌いていけばよいでしょう。

別路線

$\overrightarrow{\mathrm{OQ}}$ を得るにあたっては

• 点 $\mathrm{Q}$ は線分 $\mathrm{AP}$ を $h \ : \ 1$ に外分する点

と捉えて

$\overrightarrow{\mathrm{OQ}}=\displaystyle \frac{-\overrightarrow{\mathrm{OA}}+h\overrightarrow{\mathrm{OP}}}{h-1}$

という外分点の公式から導出してもよいでしょう。

これは

$\overrightarrow{\mathrm{OQ}}=\displaystyle \frac{h}{h-1}\overrightarrow{\mathrm{OP}}-\displaystyle \frac{1}{h-1}\overrightarrow{\mathrm{OA}}$

と見ると、

• 曲線 $C'$ は、曲線 $C$ を原点中心に $\displaystyle \frac{h}{h-1}$倍し、$-\displaystyle \frac{1}{h-1}\overrightarrow{\mathrm{OA}}$ 方向に平行移動したもの

と捉えることができます。

平行移動は長さに影響を及ぼさない操作ですから、求める曲線の長さは

• 元のアステロイド $C$ の長さの $\displaystyle \frac{h}{h-1}$ 倍

ということになり、この路線から考えてもよいでしょう。

アステロイドならではの問題について

本問はアステロイド特有の性質が前面に出ている問題ではなく、本問の趣旨を問いにしたければ、別にアステロイドじゃなきゃいけない理由もありません。

アステロイド特有の性質について確認したければ

をご活用ください。

解答はコチラ