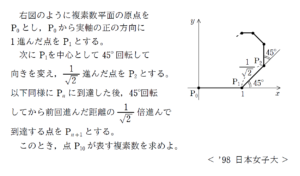
例題はこちら(画像をクリックするとPDFファイルで開きます。)

進行方向に関する決まったアルゴリズムによって定まる点列を扱う問題で、この分野の定番問題の一つです。
イメージとしてラーメンの器にある

のようなクルクルした動きのイメージです。
このラーメンの器の模様はどうやら雷紋と呼ばれているようで、勝手に雷紋問題と呼ばせてもらうことにします。
迷路のような形で悪霊が道に迷うとのことで、古くから中国で魔除けの模様として使われていたようです。
本問、及びそれに準ずる話題の問題については今日以降道に迷っていてはいけません。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
動きを立式する
今回の動きについて立式したいと思います。
回転が絡んでいますから、複素数平面で処理するのが自然でしょう。
本問は最初から複素数平面の問題として訊かれていますが、座標の問題として複素数平面の「ふの字」も書いていない場合でも、複素数平面を持ち出しましょう。
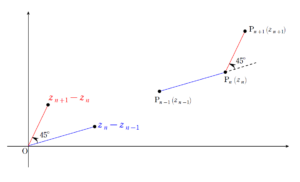
原点中心の回転の方が分かりやすいということであれば

のように、原点まで平行移動して考えればよいです。
これにより、
\((z_{n+1}-z_{n})=(z_{n}-z_{n-1})\cdot \displaystyle \frac{1}{\sqrt{2}}(\cos{45^{\circ}}+i\sin{45^{\circ}})\)
と立式できます。
これにより、等比数列の構造が現れ、一旦階差数列が求まることになり、そこから一般項に繋げることができます。
なお、
- \(\overrightarrow{ \mathrm{P_{n-1}}\mathrm{P_{n}} }\) を \(45^{\circ}\) 回転し、大きさを \(\displaystyle \frac{1}{\sqrt{2}}\) 倍したものが \(\overrightarrow{ \mathrm{P_{n}}\mathrm{P_{n+1}} }\)
と捉えることで、
\((z_{n+1}-z_{n})=(z_{n}-z_{n-1})\cdot \displaystyle \frac{1}{\sqrt{2}}(\cos{45^{\circ}}+i\sin{45^{\circ}})\)
という式にいきなり辿り着くことも可能です。
今回は \(\mathrm{P_{10}}\) という具体的な点であるため、計算量にそこまで負担はありません。
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)

例題の補間的問題です。
例題では、
日本語で書かれた動きを、漸化式を用いて立式する
という流れでしたが、類題は
漸化式が与えられて、それによって定まる点列がどのような振る舞いをするか
というニュアンスの訊かれ方をしています。
一般の \(z_{n}\) の実部虚部である \(x_{n}\) , \(y_{n}\) の計算が少し億劫ですが、最後の極限まで含めて考える要素もあり、この話題の代表的な内容を含んでいます。
ただ、カギとなる漸化式が与えられてしまうと、点列の振る舞い自体に触れることなく、漸化式の処理さえできれば最後のオチの極限まで計算できてしまいますから、そこは良し悪しでしょう。
例題の解答はコチラ
類題の解答はコチラ