問題はこちら(画像をクリックするとPDFファイルで開きます。)
平面内の長方形を回転させ、出来上がった回転体をさらに回転させるという問題です。
空間座標における回転体に習熟している必要があり、やるべきこと(目の付け所)がしっかりと自分のものになっていれば確保できますが、そうでない場合はインプットをしっかりとした上で、アウトプットをこなすことで「血となり肉となる」状態を作り上げましょう。
(以下ネタバレ注意)
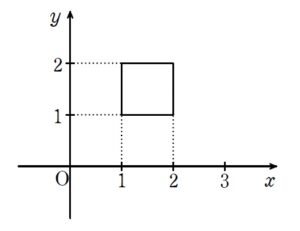
+ クリック(タップ)して続きを読む (1) については \(xy\) 平面内の長方形の \(x\) 軸回転体です。 円柱から円柱をくり抜いた立体となり、体積計算するにあたり積分計算は不要でしょう。 どちらかと言うと大学入試というよりも、高校入試レベルです。 \(V(s)\) の式を Get できれば、あとは微分して増減を調べるだけです。 計算すれば、\(s=0\) で \(V(s)\) は最大となることが分かります。 (1) で \(s=0\) のときを考えることになります。 このときの長方形 \(R_{0}\) は正方形となり、 のようになります。 これを \(x\) 軸について回転させた図形を考えますが、見やすく整理するために というように \(x \gt 0\) , \(y \gt 0\) , \(z \gt 0\) の範囲で考えることにします。 一般に 空間座標における回転体の扱い方 がポイントになる点です。 あくまで、「回転後の全体像を捨てろ」ということであり、 「回転前の全体像(何を回転させるのか)」 については把握している必要があります。 どちらが考えやすいかは言うまでもありません。 前者は先に回しているせいで、訳が分かりません。 切ってから回します。 今回のタイヤ(回転前の立体)を \(y=t\) で切ると という 2 つの場合分けが生じます。 という長方形を \(y\) 軸まわりに 1 回転させると という円環(ドーナッツ)部分が断面ということになります。 一方、 という長方形を \(y\) 軸のまわりに 1 回転させると という円環(ドーナッツ)部分が断面ということになります。 このように、回転の中心 \((0 \ , \ t \ , \ 0)\) からの 回転の中心 \((0 \ , \ t \ , \ 0)\) からの を司る ということになります。 最小距離を『取っ手』が付いていると思って、その取っ手を持ってぶん回すと考えるとイメージしやすいと思います。 空間座標における回転体の体積【円錐の回転体の体積とその工夫】【2017年度 東京大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) (1) は難関大志望者であれば、特に手が止まることはないでしょう。 点 \(P\) の軌跡が円となることも容易に把握できると思います。 問題は (2) です。 点 \(Q\) が \(OQ=1\) を満たしながら、平面 \(x=0\) を動くということは, 点 \(Q\) は原点 \(O\) を中心として平面 \(x=0\) で回転しています。 線分 \(OP\) とはいわば円錐の「母線」です。 点 \(Q\) の回転に伴って ... 空間座標における回転体【ズレて刺さった団子の回転体】【2014年度 名古屋大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 空間座標における回転体というトピックスで、難関大を目指すにあたっては避けては通れない話題です。 一般に 空間座標における回転体の扱い方 全体像を捨てろ 切ってから回す(先に回すな) 回転の中心からの最大距離・最小距離を捉える がポイントになる点です。 全体像については「仮に分かったとしても、それが体積を求めることに役に立つのか?」ということを考えれば、考えるだけ無駄です。 むしろ混乱するだけなので、考えない方がいいぐらいです。 ... 空間座標における回転体【ベビースターラーメンの回転体】【2003年度 東北大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 空間座標における回転体は出題されれば差が付くトピックスです。 難関大を目指すにあたってはしっかりと準備しておきたい話題ですので、しっかりとマスターして周りの受験生に差をつけましょう。 一般に 空間座標における回転体の扱い方 全体像を捨てろ 切ってから回す(先に回すな) 回転の中心からの最大距離・最小距離を捉える がポイントになる点です。 全体像については「仮に分かったとしても、それが体積を求めることに役に立つのか?」ということを ... 仮想難関大(オリジナル予想問題)【微積分~空間座標における回転体】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 仮想難関大シリーズということで、東大、京大をはじめとする旧帝大、東工大、国公立大学医学部医学科などの難関国公立大を想定したオリジナルの自作問題です。 「手垢の付いていない問題で最後の力試しがしたい」 という方はぜひご活用ください。 本問は最初は \(z\) 軸回転として作ろうと思っていましたが、よくよく考えると \(z\) 軸回転だと円錐 ということになり、問題としては面白くなかったので、\(y\) 軸回転体にしま ... 斜軸回転体の体積【傘型積分】【コーン積分】【2006年度 横浜国立大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 斜軸回転体の体積というテーマ性のある話題です。 通常の \(x\) 軸回転体、\(y\) 軸回転体に加え、マスターしておきたい話題のひとつでしょう。 斜軸回転体の試験場(記述式)での倒し方は次のいずれかです。 斜軸回転体の倒し方 ①:回転軸に対して垂直に切り、変数変換(置換積分) ②:回転軸を回転させて \(x\) 軸に重ねる。 ※ 傘型分割というイキった解法もありますが、順番的には① , ② をきちんとマスターすべきです。 ... 縦軸回転体の体積【バームクーヘン分割】【2004年度 京都工芸繊維大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 縦軸回転体の体積をシンプルに問いかけている潔い問題です。 もちろん 単調性のある\(y\) 軸回転体の体積については \(\displaystyle\int_{a}^{b}\pi x^{2} dy\) という \(y\) 軸回転体の体積の公式をそのまま使えばいいのですが、単調性のある曲線ばかりではなく、「くり抜き」が必要な問題も多く出題されています。 手際よく処理していくことが求められます。 さすがに \((\lo ... 仮想難関大(オリジナル予想問題)【微積分~回転体についての総合問題~】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 仮想難関大シリーズということで、東大、京大をはじめとする旧帝大、東工大、国公立大学医学部医学科などの難関国公立大を想定したオリジナルの自作問題です。 「手垢の付いていない問題で最後の力試しがしたい」 という方はぜひご活用ください。 今回は東大がよく出題する空間図形問題を意識してみました。 平面の方程式が厳密には範囲外であることについてはもちろん分かっています。 そして、それを回避するような問題文に変えることもできたのですが、そうすると若干この ... 2021年度 九州大学理系第3問【絶対不等式の考え方】【x軸回転体の体積】 問題はこちら(画像をクリックするとPDFファイルで開きます。) テーマとしては (1) が絶対不等式の考え方、(2) が x 軸回転体の体積ということですが、実質は (1) が山場です。 区間 \(I\) において \(f(x) \gt c\) ( \(c\) は定数 ) が常に成立するとは 区間 \(I\) における最小値を \(m\) として \(m \gt c\) が成立する。 ということが言えます。 その区間における最小値(一番雑魚)が \(c\) に勝てるのであれば、その他の連 ... 180°しか回転しない空間座標の回転体の体積【2009年度 東京大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 通常の空間座標における回転体の体積自体、東大は好んで出題する傾向にありますが、本問は 180°しか回転しない回転体の体積 について扱います。 このような「こうなったらどうする?」という味付けは教育的で、いかにも東大らしい良問だと思います。 とは言え、難易度という点では少しハードかなとは思います。 初見の方はぜひ考えてみてください。 (以下ネタバレ注意) + クリック(タップ)して続きを読む イメージ図について のようなイメージで ... 回転体の回転体【タイヤの回転体】【2011年度 名古屋大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 平面内の長方形を回転させ、出来上がった回転体をさらに回転させるという問題です。 空間座標における回転体に習熟している必要があり、やるべきこと(目の付け所)がしっかりと自分のものになっていれば確保できますが、そうでない場合はインプットをしっかりとした上で、アウトプットをこなすことで「血となり肉となる」状態を作り上げましょう。 (以下ネタバレ注意) + クリック(タップ)して続きを読む (1) について (1) については \(xy ... 有名曲線【トロコイド】【2012年度 お茶の水女子大学ほか】 例題はこちら(画像をクリックするとPDFファイルで開きます。) 類題はこちら(画像をクリックするとPDFファイルで開きます。) トロコイドという有名曲線を扱った問題です。 トロコイドとは 円が滑らずに転がったときの円の内部または外部の定点の軌跡 です。 円周上の定点の軌跡はサイクロイドと呼ばれる有名曲線です。 基本的にはサイクロイドに準ずる態度でトロコイドのパラメータ表示を得ていきます。 ひとまずサイクロイドに関してまだ足元がグラグラということであれば でサイクロイドについての問題を扱っています。 (以下 ... 2023年度 東京大学理系第6問【条件を満たす線分と折れ線の先端の存在領域の体積】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 見るからに威圧感のある空間図形の問題です。 問題を噛み砕くのに時間がかかり、突破口を見出すのに時間がかかり、それを計算処理するのに時間がかかり、適切な文章や図でまとめるのに時間がかかり、というようにとにかく時間がかかります。 面白い問題だとは思いますが、試験場では相手にしてはいけない問題です。 結局は (1) では棒、(2) ではヌンチャク(折れ線) が立方体の表面と共有点をもたないように動くときの先端の存在領域を考えることになります。 また ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) 空間における三角形の回転体の体積というシンプルな題意です。 空間座標における回転体の体積は東大頻出のトピックスで、凝ったものから標準的なものまで出題されてきましたが本問は標準寄りの問題です。 過去問を通じて演習を積み、しっかりと仕上げてきた受験生であれば心理的に慌てずに立ち向かえたと思います。 一般に 空間座標における回転体の扱い方 全体像を捨てろ 切ってから回す(先に回すな) 回転の中心からの最大距離・最小距離を捉える がポイントになる点で ... 気になるものがあればご活用ください。(1) について
(2) について

空間座標の回転体の処方箋
※ 全体像を捨てろと言っているのに絵を描いたじゃないかと言う人へ
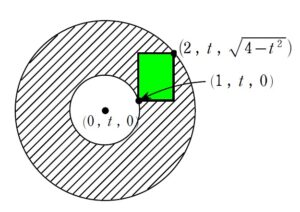
切ってから回す(先に回すな)
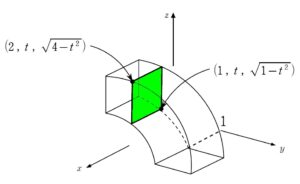
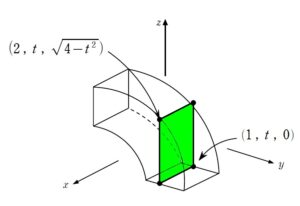
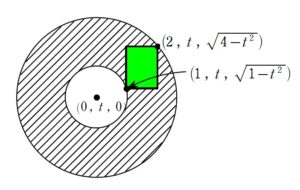
回転の中心からの最大距離・最小距離を捉える


場数を踏みたい方へ














