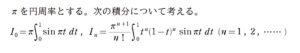(1) について
\(f_{n}(x)=1+\displaystyle \frac{x}{1!}+\displaystyle \frac{x^{2}}{2!}+\cdots+\displaystyle \frac{x^{n}}{n!}\) とおいたとき
\(f'_{n+1}(x)=1+\displaystyle \frac{x}{1!}+\displaystyle \frac{x^{2}}{2!}+\cdots+\displaystyle \frac{x^{n}}{n!}=f_{n}(x)\)
という \(e^{x}\) のマクローリン展開を元にしたカラクリは手垢が付いたカラクリです。
今回は「数学的帰納法によって」という指示がありますが、この指示が余計なお世話に思えてほしいところです。
後半の内容については被積分関数が、積分区間 \(0 \leq t \leq 1\) において、
\(t^{n} (1-t)^{n} \sin{\pi t} \leq 1\)
であることを利用して
\(I_{k} \lt \displaystyle \frac{\pi^{k+1}}{k!}\)
と上から押さえることができれば、前半で示した不等式の活用が見込めます。
(2) について
積分漸化式の作成の際の常套手段
部分積分からの積分漸化式の作成
という路線を外したくありませんし、この方針は明確に見えてほしい基本です。
ただし、やってみると分かると思いますが、相当計算が重たいです。
「置き換え」を駆使しながら少しでも目に優しくしましょう。
自分のためでなく、読む側である採点者のためにも。
(3) について
矛盾までの道筋まである程度見せてくれているので、前の設問も見返しながら、どう結び付くのかを考えていきます。
(2) で得た \(I_{n}\) についての漸化式のおかげで、\(A_{n}(=p^{n}I_{n})\) についての漸化式も得ることになり、\(I_{n} \gt 0\) ということも併せると \(A_{n}\) が帰納的に正の整数であることが見えてきます。
(1) がどう効いてくるかという視点で、(1) の活用を考えてみると
\(A_{0}+A_{1}+A_{2}+\cdots+A_{n} \lt \pi e^{\pi}\)
であることが分かります。
正の整数を加え続けていって、有限確定値未満ということがおかしなことだと気が付けばハッピーエンドです。
総合的に
レールを敷いてくれているという点で、発想力というよりは
- 定番の手法を活かせるかという運用力
- 誘導を活かせるかという活用力
- 見据えた方針を処理しきる計算力と集中力
という力が問われます。
特に計算についてはかなり重たいです。
ただ、この重たい計算の果てに、「\(\pi\) が無理数であるということが証明できる」という結果が待っていたことを考えると、やった甲斐があったと感じるのではないでしょうか。
歴史的には
ネイピア数 \(e\) が無理数であることを最初に証明した人物は、かの有名な「オイラー」です。
それに対し、円周率 \(\pi\) が無理数であることを最初に証明した人物は「ランベルト」と言われています。
ネイピア数 \(e\) が無理数であることの証明については
-

-
eが無理数であることの証明【微分の利用、定積分の利用】【1997年度 大阪大学ほか】
問題はこちら(画像をクリックするとPDFファイルで開きます。) ネイピア数 \(e\) が無理数であることを証明させるという、先人の重みを感じるような問題です。 もちろん、誘導なしで証明 ...
続きを見る
で扱っています。
解答はコチラ