例題はこちら(画像をクリックするとPDFファイルで開きます。)
面積評価と極限に関する問題です。
現役生にとって、数Ⅲの完成度は大きく合否を左右します。
そんな中で、今回の話題はきっちりと差が付くテーマです。
本問、及び類題を用いて面積評価の使いどころと一連のストーリーをしっかりと押さえましょう。
(以下ネタバレ注意)
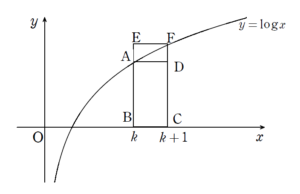
+ クリック(タップ)して続きを読む 今回評価する \(\displaystyle \sum_{k=1}^{n}\log{k}\) は、和の形です。 和の形を評価したいときの有力手段の一つとして「面積評価」という方法があります。 長方形 \(\mathrm{ABCD}\) の面積が \(\log{k}\) であり、長方形 \(\mathrm{EBCF}\) の面積が \(\log{(k+1)}\) です。 \(\log{k} \lt \displaystyle \int_{k}^{k+1}\log{x} dx \lt \log{(k+1)}\) と評価し、\(k\) の範囲に気を付けながら \(\displaystyle \sum_{ \ }^{ \ } \) すればよいでしょう。 (1) で得た不等式を用いて極限計算をするという本問の流れから はさみうちの原理 がオチであることを想定しておきたいですね。 今回は \(n!\) にまつわる極限ですが、 \(\displaystyle \sum_{k=1}^{n}\log{k}=\log{(n!)}\) と見ることになります。 そうなると (1) は \(n\log{n}-n+1 \lt \log{(n!)} \lt (n+1) \log{n}-n+1\) と見ます。 \({(n!)}^{\frac{1}{n \log{n}}}\) を登場させるために、辺々 \(\displaystyle \frac{1}{n\log{n}}\) をかけることで \(1-\displaystyle \frac{1}{\log{n}}+\displaystyle \frac{1}{n \log{n}} \lt \log{(n!)}^{\frac{1}{n\log{n}}} \lt 1+\displaystyle \frac{1}{n}-\displaystyle \frac{1}{\log{n}}+\displaystyle \frac{1}{n \log{n}}\) を得ます。 最左辺、最右辺の極限はどちらも \(1\) となりますから、はさみうちの原理で解決します。 本問は \(\displaystyle \sum_{k=1}^{n} \log{k}=\log{(n!)}\) と計算できましたが、 ということも基本的対応になりますので、ぜひ押さえておきましょう。 例題で学んだ流れやシナリオが自分のものになっているかを確認するのにうってつけの類題です。和の形の評価
(2) について
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)


