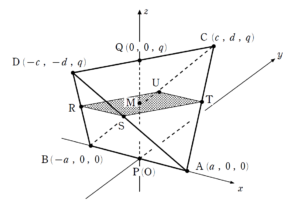
問題はこちら(画像をクリックするとPDFファイルで開きます。)
京大が定期的に出題する四面体に関する論証問題です。
幾何・座標・ベクトルという3分野が考えられますが、本問は必要に合わせてどの分野のまな板の上で調理するかを柔軟に対応する力が養えます。
難易度としてはやや難でしょうが、得られるものは大きい問題です。
美しく解く方法もありますが、愚直にやってできないことはありません。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 色々考えられますが、ベクトルを導入し、内積が \(0\) ということを目指す路線で行きたいと思います。 \(\overrightarrow{ \mathrm{AB} }=\vec{b}\) , \(\overrightarrow{ \mathrm{AC} }=\vec{c}\) , \(\overrightarrow{ \mathrm{AD} }=\vec{d}\) と主役の3本(基底)を設定します。 まず、中点の位置ベクトル \(\overrightarrow{ \mathrm{AP} }\) , \(\overrightarrow{ \mathrm{AQ} }\) は \(\overrightarrow{ \mathrm{AP} }=\displaystyle \frac{1}{2} \vec{b}\) , \(\overrightarrow{ \mathrm{AQ} }=\displaystyle \frac{1}{2} \vec{c}+\displaystyle \frac{1}{2} \vec{d}\) であり、 \(\overrightarrow{ \mathrm{PQ} }=\overrightarrow{ \mathrm{AQ} }-\overrightarrow{ \mathrm{AP} }\) ですから \(\overrightarrow{ \mathrm{PQ} }=-\displaystyle \frac{1}{2} \vec{b}+\displaystyle \frac{1}{2} \vec{c}+\displaystyle \frac{1}{2} \vec{d}\) を得ます。 これにより、 \(\overrightarrow{ \mathrm{PQ} } \cdot \overrightarrow{ \mathrm{AB} }=-\displaystyle \frac{1}{2} |\vec{b}|^{2}+\displaystyle \frac{1}{2} \vec{b} \cdot \vec{c}+\displaystyle \frac{1}{2} \vec{b} \cdot \vec{d}\) となります。 もちろん、このあと\(\overrightarrow{ \mathrm{PQ} } \cdot \overrightarrow{ \mathrm{AB} }=0\) を目指していくことになります。 そこに辿り着くための条件が ということになります。 条件の対称性から という図で考えても問題ありません。 目指すべきは 点線部分の体積=実線部分の体積 ということですが、それぞれの立体を直接計算して「ほ~ら同じでしょ」ともっていくのはスジが悪いと言わざるを得ません。 そこで、 ということを目指すことにします。 つまり、全体との体積比を考えるわけです。 そこで、\(\mathrm{R}\) , \(\mathrm{S}\) が、それぞれ 辺 \(\mathrm{BC}\) , \(\mathrm{AD}\) をどのような内分比で分けるのかについて調べていくことになります。 もちろん、そこに迫るには ということを立式していくことになるでしょう。(いわゆる共面条件) ここからはスタミナが必要な処理になります。 詳しくは【解1】をご覧ください。 実は のように実線部の立体を \(180^{\circ}\) 回転させると、点線部の立体に重なります。 上述の方針1において を調べたところで、この事実に気が付く人は気が付きます。 ただ、気が付かなかったら方針1で引き続き進めればよいです。 のように、(1) の直交性をうまく利用して座標軸を設定することで、体積の2等分という目標を、断面積の2等分という目標に言い換えることができます。 直線 \(\mathrm{PQ}\) というのが 「糸のような刃物」 だと思ってください。 線分 \(\mathrm{PQ}\) を含む平面で切る という問題文の条件は と言い換えることができるでしょう。 (ウォーターカッターのようなイメージ) それによって今回の四面体を切断すると思ってください。 四面体が切断されるとともに、断面積も切断されているイメージがもてるでしょうか? 実は断面(上の図でいう四角形 \(\mathrm{RSTU}\) )は平行四辺形になり、\(\mathrm{M}\) はその中心となります。 そりゃ断面積も2等分だわ となるでしょう。 もちろん解答では四角形 \(\mathrm{RSTU}\) が平行四辺形であることをきちんと述べていきます。 なお、 断面積が常に等しいならば、その2つの立体の体積も等しい という事実は「カバリエリの原理」と呼ばれます。 この路線は【解3】をご覧ください。(1) について
(2) について
方針1:体積比を考える
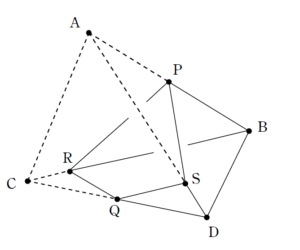
方針2:2つの立体が合同であることを見抜く
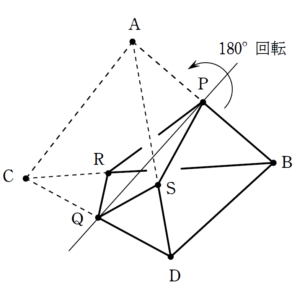
方針3:座標を設定して断面積を考える。