問題はこちら(画像をクリックするとPDFファイルで開きます。)
正射影ベクトルの扱いから入り、そこから整数問題チックなオチに着地するという気持ちの良い問題です。
ただし、(1) の正射影ベクトルの扱いで躓いてしまうと、(2) , (3) まで進めないため、最後のオチのキレイさを感じることはできません。
(以下ネタバレ注意)
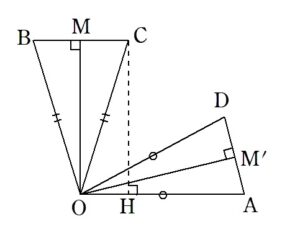
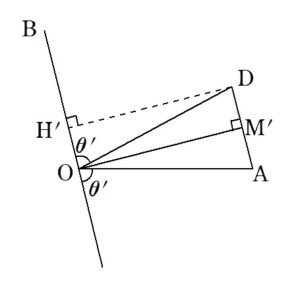
+ クリック(タップ)して続きを読む 正射影ベクトルについて というように \(\vec{b}\) を \(\vec{a}\) の方向に正射影した正射影ベクトルを \(\vec{b'}\) とします。 まずそもそも \(\vec{b'}\) は \(□ \ \vec{a}\) という形で表せるに決まっている という気持ちが大切です。 この、 \(\vec{b'}\) を得る第1歩目は \(\vec{b'}=\displaystyle \frac{\vec{a}}{|\vec{a}|} \times |\vec{b}| \cos{\theta}\) という式です。 単位ベクトル(大きさが1のベクトル)を「影の長さ倍」したと考えます。 これを整理すると \(\vec{b'}=\displaystyle \frac{|\vec{b}|\cos{\theta}}{|\vec{a}|} \times \vec{a}\) と変形できます。 ここから、\(|\vec{a}| \ |\vec{b}| \ \cos{\theta}=\vec{a} \cdot \vec{b}\) という内積をインスピレーションすると \(\vec{b'}=\displaystyle \frac { |\vec{a}| |\vec{b}| \cos{\theta} } { |\vec{a}|^{2} } \times \vec{a}\) と変形したくなると思います。 最終的に \(\vec{b'}=\displaystyle \frac { \vec{a} \cdot \vec{b} } { |\vec{a}|^{2} } \times \vec{a}\) と、内積を用いて正射影ベクトルを表すことができます。 本問の構図は 本問の状況を簡単に図で表してみると といった感じでしょうか。 \(\overrightarrow{ OC }\) が欲しいので、\(\overrightarrow{ OH }\) という正射影ベクトルが分かれば解決ということになります。 同様に \(\overrightarrow{ OD }\) が欲しければ のように、\(\overrightarrow{ OH' }\) という正射影ベクトルをゲットできれば解決です。 この後の (2) , (3) は手なりに進められるはずです。 特に最後の (3) のオチは気持ちよい着地の仕方をします。 類題 類題というか、ほぼ同じ問題が出題されていたので紹介しておきます。 本問は結構個性の強い問題でカブるようなことはないと思っていたのですが \(\cdots\)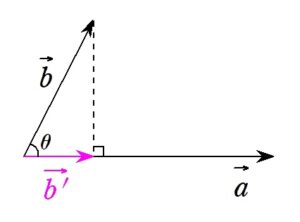
類題はこちら(画像をクリックするとPDFファイルで開きます。)


