問題はこちら(画像をクリックするとPDFファイルで開きます。)
表向きは座標の標準問題、あるいは軌跡の問題の標準問題に見えますが、円の反転変換を題材にした問題で、入試においては高い頻度で登場する話題です。
古典的な内容であるため、考え方や流れにおいて、それなりにクセがあります。
特にオチである点 \(Q\) の軌跡については、一歩間違えると「どないすんねん」と身動きがとれなくなってしまいかねません。
逆に勉強してきた人からすれば「いただきます」と美味しく完答できるでしょう。
以下少し記事が長いので、興味のあるところについて「+マーク」をクリック(タップ)して読んでください。
+ 本問について続きを読む よくある手立てとしては \(\overrightarrow{ OQ }=k\overrightarrow{ OP } \cdots ①\) と見立てて、ベクトルの成分経由で座標を求める方法です。 \(P \ ( x_{0} \ , \ y_{0} )\) が既知のものとして、\(\overrightarrow{ OQ }\) を求めるためには倍率 \(k\) を求める必要があります。 普通は \(OP \cdot OQ=1\) という関係式を用いて倍率 \(k\) を求めるのですが、今回はそれが「証明すべきこと」になっていますから、ここでは一旦 \(OP \cdot OQ=1\) という関係を認めたうえで話を進めていきます。 \(|\overrightarrow{ OQ }|=k|\overrightarrow{ OP }|\) ですから両辺 \(|\overrightarrow{ OP }|\) をかけると、 \(1=k|\overrightarrow{ OP }|^{2}\) という関係を得て、\(k=\displaystyle \frac{1}{|\overrightarrow{ OP }|^{2}}\) と \(k\) が求まります。 そして、\(①\) から \(\overrightarrow{ OQ }=\displaystyle \frac{1}{|\overrightarrow{ OP }|^{2}}\overrightarrow{ OP }\) を得るので、\(\overrightarrow{ OQ }\) の成分を Get できます。 ただ、あくまでこれは、\(OP \cdot OQ=1\) を認めた上での話で、今回これは証明すべきことです。 これを示すには、 という図において \(\triangle OQT_{1}\) と \(\triangle OT_{1}P\) が相似であることを用いれば求めることができます。 (2)においては点 \(Q\) の軌跡です。 \(x_{1}\) , \(y_{1}\) は好き勝手な値をとることはできず、何か縛りがあります。 この \(x_{1}\) , \(y_{1}\) を縛っている関係式を Get しにいくというのが軌跡の考え方の基本です。 この関係式を Get するシナリオは $$\begin{eqnarray} という関係式から $$\begin{eqnarray} という関係式に直して、\(x_{0}\) , \(y_{0}\) を縛っている関係式 ( 今回は \(x_{0}+y_{0}=2\) ) に代入して、\(x_{1}\) , \(y_{1}\) を縛っている関係式を Get するというシナリオです。 今回の場合は $$\begin{eqnarray} から \(x_{0}=\) , \(y_{0}=\) とやりたいところですが、この式からそこまでもっていくのは初見だと「どないすんねん」となる可能性が高いでしょう。 ベクトル経由で考えていれば、(1) では \(\overrightarrow{ OQ }=\) という形で見ていましたが、今度は \(\overrightarrow{ OP }=\) という形で考えれば $$\begin{eqnarray} という形にもっていけそうですね。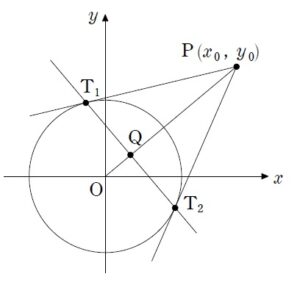
\left\{
\begin{array}{l}
x_{1} = x_{0} , y_{0} の式 \\
y_{1} = x_{0} , y_{0} の式
\end{array}
\right.
\end{eqnarray} $$
\left\{
\begin{array}{l}
x_{0} = x_{1} , y_{1} の式 \\
y_{0} = x_{1} , y_{1} の式
\end{array}
\right.
\end{eqnarray} $$
\left\{
\begin{array}{l}
x_{1} = \displaystyle \frac{x_{0}}{x_{0}^{2}+y_{0}^{2}} \\
y_{1} = \displaystyle \frac{y_{0}}{x_{0}^{2}+y_{0}^{2}}
\end{array}
\right.
\end{eqnarray} $$
\left\{
\begin{array}{l}
x_{0} = \\
y_{0} =
\end{array}
\right.
\end{eqnarray} $$
+ 反転について続きを読む 今回話題になっている反転についてまとめておきます。 反転 中心 \(O\) , 半径 \(r\) の円において2点 \(P\) , \(Q\) を次のように定める。 特に、\(P\) を定めて、それに応じて点 \(Q\) が定まるというように見たとき、この \(P\) → \(Q\) という変換を反転変換と言う。 \(P\) の動きに伴って、点 \(Q\) も動いていきますが、このとき点 \(P\) の軌跡が直線、または円のときの反転写像( \(Q\) の軌跡)についてまとめると次のようになります。 反転写像の円円対応 原点を通る直線 \(\longrightarrow\) 原点を通る直線 原点を通らない直線 \(\longrightarrow\) 原点を通る円 原点を通る円 \(\longrightarrow\) 原点を通らない直線 原点を通らない円 \(\longrightarrow\) 原点を通らない円 ※円円対応とは、『直線も「半径が無限大の円」と見なせば、円は円に対応すると見なせる』ということです。 円円対応については、入試においては覚えておいて損はないかなぐらいのもので、無理して覚える必要はないと思います。 その代わり、問題を解く際の流れやシナリオについてはしっかりと頭に入れておく必要があります。 本問は 原点を通らない直線 \(\longrightarrow\) 原点を通る円 というパターンだったので、他のパターンの類題をもってきました。 ただし、 原点を通る直線 \(\longrightarrow\) 原点を通る直線 については自分自身に移る変換なので、ある意味自明で面白みに欠けますので省きました。 シナリオはほぼ一緒ですので、名古屋大学の例題で詳しい考え方などを解説した分、略解となっています。 ご了承ください。 無理に全部やる必要はありませんが、定着用に適宜ご利用いただければと思います。
(なんのこっちゃと言う人は別に無視してかまいません。)
+ 類題について続きを読む 例題の問題 ( '07 名古屋大学 ) とほぼ同じ問題です。 \(OP \cdot OQ=1\) が隠れているため、自分で見出す必要がある点が経験が必要かもしれません。 問題設定の与えられ方が反転の定義に忠実な与えられ方をしています。 \(Q\) の座標を \((X \ , \ Y)\) とおきます。 「対称」という言葉が入っているため、例題 ( '07 名古屋大学 ) に対して、わずかながら $$\begin{eqnarray} とする際に対称性を意識しやすいかもしれません。 文字を含んだ計算になりますが、基本的なシナリオは同じです。 怯まずに計算しきってください。類題はこちら(クリックするとPDFファイルで開きます)
\left\{
\begin{array}{l}
X = x , y の式 \\
Y = x , y の式
\end{array}
\right.
\end{eqnarray} $$
(とは言え、経験がないと苦しいっちゃ苦しいですが。)




