問題はこちら(画像をクリックするとPDFファイルで開きます。)
正八面体の辺ベクトルについての論証問題であり、一見するとどこから手を付けていいのかが分かりにくい問題でしょう。
題意の主張が当たり前じゃんと思える人もいるでしょうが、どのように記述でまとめるかで悩むかもしれません。
解答自体は短く終わりますが、手も足も出ない人がいてもおかしくはないと思います。
(以下ネタバレ注意)
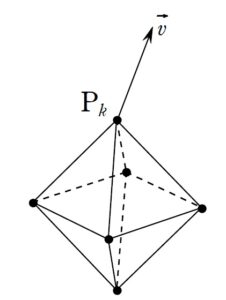
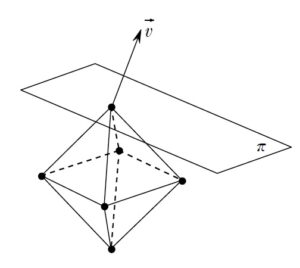
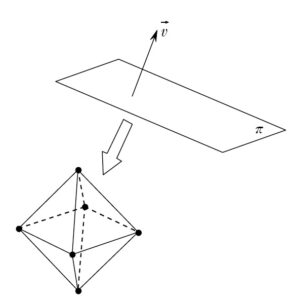
+ クリック(タップ)して続きを読む 一般に2つのベクトル \(\vec{a}\) , \(\vec{b}\) のなす角 \(\theta\) に対して、 \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\theta}\) であるため、 ということが言えます。 つまり、内積が負というのは、 なす角が鈍角 ということです。 ベクトルというのは位置によりませんから、\(\vec{v}\) の始点を正八面体の頂点の一つに重ねることができるわけです。 このとき、 というように、\(\vec{v}\) となす角が全て鈍角となるような辺ベクトルの起点 \(\mathrm{P}_{k}\) が存在することを示すわけです。 これについては、ちょうど \(\vec{v}\) を法線ベクトルにもつ平面を書き添えると明確で、 のような状態を作れることを言えばよいことになります。 ここまでくると、もはや題意の主張が当たり前のように感じることでしょう。 というように \(\vec{v}\) を法線ベクトルにもつ平面 \(\pi\) を徐々に近づけると というように \(\pi\) と、この正八面体は 1点を共有する ということになります。 ある点 \(\mathrm{O}\) をとったとき、\(\overrightarrow{\mathrm{P}_{k}\mathrm{P}_{m}} \cdot \vec{v} \lt 0\) というのは \((\overrightarrow{\mathrm{OP}_{m}}-\overrightarrow{\mathrm{OP}_{k}}) \cdot \vec{v} \lt 0\) すなわち \(\overrightarrow{\mathrm{OP}_{m}} \cdot \vec{v} \lt \overrightarrow{\mathrm{OP}_{k}} \cdot \vec{v}\) ということです。 つまり、正八面体の頂点 \(\mathrm{P}_{1}\) , \(\mathrm{P}_{2}\) , \(\cdots\) , \(\mathrm{P}_{6}\) に対して、\(\overrightarrow{\mathrm{OP}_{1}} \cdot \vec{v}\) , \(\overrightarrow{\mathrm{OP}_{2}} \cdot \vec{v}\) , \(\cdots\) , \(\overrightarrow{\mathrm{OP}_{6}} \cdot \vec{v}\) の中で最大のものを \(\overrightarrow{\mathrm{OP}_{k}} \cdot \vec{v}\) とすれば、\(k\) 以外の任意の \(m\) に対して \(\overrightarrow{\mathrm{OP}_{m}} \cdot \vec{v} \lt \overrightarrow{\mathrm{OP}_{k}} \cdot \vec{v}\) ということが言えて解決です。内積の符号とベクトルのなす角

路線2:式的に示す

