例題はこちら(画像をクリックするとPDFファイルで開きます。)
決して派手な問題ではありませんが、ベクトルに関する基本的な扱いを要求し、最後は面積比の最小問題がオチという実戦的な演習問題です。
角度を共有する三角形の面積比については手際よく立式したいところです。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む \(\overrightarrow{\mathrm{OG}}\) についてですが、\(k\) 倍する前の \(\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}\) は定ベクトルです。 イメージとしては というように、定ベクトルの伸縮で \(\mathrm{G}\) の位置が決まるイメージです。 \(\mathrm{G}\) が \(\triangle{\mathrm{OAB}}\) の内部ということなので、線分 \(\mathrm{AB}\) の中点 \(\mathrm{M}\) に注目し \(\overrightarrow{\mathrm{OG}}=□ \overrightarrow{\mathrm{OM}}\) というように、\(\overrightarrow{\mathrm{OM}}\) の伸縮と見て、この倍率 \(□\) が \(0 \lt □ \lt 1\) というように処理すればよいでしょう。 \(\mathrm{G}\) , \(\mathrm{P}\) , \(\mathrm{Q}\) が同一直線上にあるということの翻訳については色々ありますが、今回は \(\overrightarrow{\mathrm{OG}}=s\overrightarrow{\mathrm{OP}}+t\overrightarrow{\mathrm{OQ}}\) と表したとき \(s+t=1\) という形で翻訳します。 角度を共有する三角形の面積比 \(\displaystyle \frac{\triangle{\mathrm{OPQ}}}{\triangle{\mathrm{OAB}}}\) については というように共有する角度を \(\theta\) とおくと $$\begin{eqnarray} とシンプルに立式できます。 (2) から \(k=\displaystyle \frac{pq}{p+q}\) という結果が得られ、\(k=\displaystyle \frac{1}{4}\) という条件から \(p+q=4pq\) という関係式を得ます。 この条件の下で \(pq\) の最小値を求めることになります。 積と和に関する関係式が得られているところから、相加平均・相乗平均の関係が目に付けばそちらから攻め落とす方針が考えられます。 \(p+q=4pq\) という関係式から、 \(q=\displaystyle \frac{p}{4p-1}\) と文字消去できます。 したがって、 \(pq=\displaystyle \frac{p^{2}}{4p-1}\) と、1変数関数を処理すればよいことになります。 注意したいのは \(p\) の範囲です。 単純に \( 0 \lt p \lt 1\) として処理すると誤りで、 という2点より \( 0 \lt \displaystyle \frac{p}{4p-1} \lt 1\) という不等式が得られます。 ここから得られる \(p\) の範囲を考えないといけません。 \(q\) は消えますが、生前持っていた \( 0 \lt q \lt 1\) という条件を引き継がせないといけないわけです。 文字消去する際に気を付けたいポイントです。 (2) が最小値ではなく、とり得る値の範囲を要求しているため、最後のオチで相加・相乗平均の関係は使えません。(1) について
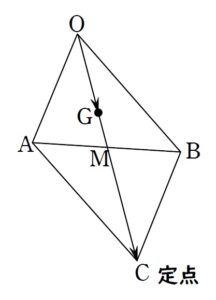
(2) について
(3) について
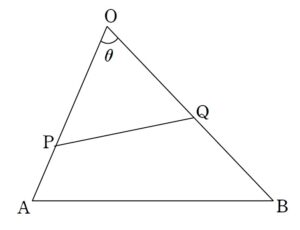
\displaystyle \frac{\triangle{\mathrm{OPQ}}}{\triangle{\mathrm{OAB}}} &=& \displaystyle \frac{\displaystyle \frac{1}{2} \cdot |\overrightarrow{\mathrm{OP}}| \cdot |\overrightarrow{\mathrm{OQ}}|}{\displaystyle \frac{1}{2} \cdot |\overrightarrow{\mathrm{OA}}| \cdot |\overrightarrow{\mathrm{OB}}|} \\
&=& \displaystyle \frac{p|\overrightarrow{\mathrm{OA}}|q|\overrightarrow{\mathrm{OB}}|}{|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|}\\
&=&pq
\end{eqnarray}$$路線1:相加平均・相乗平均の関係
路線2:文字消去からの微分
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)


