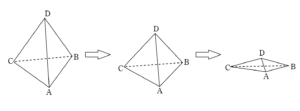
例題はこちら（画像をクリックするとPDFファイルで開きます。）
類題１はこちら（画像をクリックするとPDFファイルで開きます。）
類題２はこちら（画像をクリックするとPDFファイルで開きます。）
頂点を結ぶ線分が「通れるか通れないか」がランダムに決まり、最終的にある頂点からある頂点へ「到達可能か」を考える問題です。
今回３題もってきましたが、扱う図形は様々です。
様々であるがゆえにマニュアル的な態度ではなく、その図形的特徴を考慮してその場で急所を掴んでいく
「その場力」
がものを言う問題でしょう。
例題は軽めですが、徐々に急所やエッセンスが濃くなるような類題を準備しました。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む
例題について
例題はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
(1) について
左側の三角形 ABC だけで考えるので、全部考えても 2^{3}=8【通り】なのでタカが知れています。
手なりに見える路線は
- S_{1} が青（通れる）か、赤（通れない）か
という観点で場合分けをすればよいでしょう。
(2) について
「対称性」ということが本問の急所でしょう。
C から D へ通れる必要があるのは当然です。
A から C に辿り着く確率と、D から F へ辿り着く確率を考えればよいわけですが、この両者は同じです。
類題１について
類題１はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
例題のパワーアップバージョンです。
(1) について
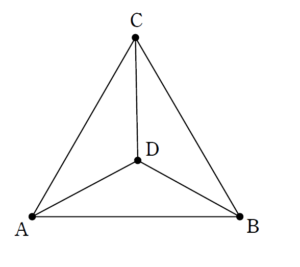
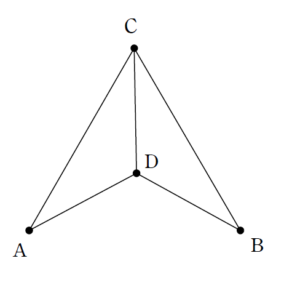
電線が３次元に張り巡らされているわけですが、
と頂点 D を地面に落としていって、
という平面回路で考えても問題ありません。
普通は
A から B まで辿り着けるかを考える際、目につくのは
- 線分 AB が通れるか通れないか
という観点での場合分けです。
AB が通れる場合、残りは知ったこっちゃありませんから、確率は p ということになります。
問題は AB が切れているときです。
という状況において
- A \to C \to B が繋がっている
- A \to D \to C \to B が繋がっている
- A \to C \to D \to B が繋がっている
などと数えられそうですが、もちろんこの中には重複が発生していたりして、大騒ぎになります。
場合分けの労力
こうしてみると、
- 線分 AB が繋がっているか切れているか
という場合分けは、本問の急所ではないことが分かります。
言わば、
「全部で１０ある困難を、１と９に振り分ける」
ような場合分けです。
労力を最小限にするには
「５と５に振り分ける」
ような場合分けが望ましいでしょう。
そうなると場合分けの急所は線分 \cdots ？
類題２について
類題２はこちら（画像をクリックするとPDFファイルで開きます。）
本問は上記の通れるか通れないかにおけるパズル的な頭の使い方に加え、
直接考えるか余事象を考えるか
という判断が大切になります。
あともう一つ大切なエッセンスを含んでいますが、それはここでは伏せておきますので、考えた後の【総括】で振り返ってみてください。