例題はこちら(画像をクリックするとPDFファイルで開きます。)
類題1はこちら(画像をクリックするとPDFファイルで開きます。)
類題2はこちら(画像をクリックするとPDFファイルで開きます。)
類題3【腕試し用類題】はこちら(画像をクリックするとPDFファイルで開きます。)
場合の数や確率の分野に対する苦手意識をもつ人を量産するタイプの問題です。
何を区別して何を区別しないか
について例題から徐々にステップアップしていき、最終的には東大後期の問題を倒してみたいと思います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 例えば、 \((1人 \ , \ 1人 \ , \ 4 人)\) , \((1人 \ , \ 4人 \ , \ 1 人)\) , \((4人 \ , \ 1人 \ , \ 1 人)\) を というようには数えません。 部屋に区別がないため、 と数えるわけです。 今度は (1) と違い、 と数えます。 つまり、(1) で考えたものの並び替えが発生することになります。 人にも部屋にも区別があります。 やはり区別があった方が考えやすいでしょう。 人にはゼッケンをつけてもらいましょう。 部屋は \(\mathrm{A}\) , \(\mathrm{B}\) , \(\mathrm{C}\) と名前を付けます。 1番さんから6番さんまでの各々は \(3\) 通りの選択肢がありますから、 \(3^{6}\) 通り の部屋割りが考えられます。 通常このまま \(3^{6}\) 通りを答えとする問題もありますが、本問の場合は 空部屋の存在を許さない という設定です。 そこで というケースを \(3^{6}\) 通りから除外することになります。 例題で鍛えてほしいのは考え方や数え方もそうですが、 何を1(い~ち)と数えるか という把握力です。 何をどういった要領で数えるのかを把握する力(問題を把握する力) という根本的な力がないと、場合の数や確率の分野は苦手なままです。 あぁ~、こういう趣旨でこういう要領で数えていけばいいのね と判断した後に \({}_n \mathrm{ P }_k\) だの、\({}_n \mathrm{ C }_k\) だのといった公式の運用が求められるわけです。 「聞けば分かる」と、「自分でできる」の差は、この問題把握力の部分でしょう。 この問題把握力をつけるためには、やはり手を動かして実験し、要領を掴むことです。 何が訊かれているか把握できるから、どう考えたらいいのかが判断できる というのは当たり前なことですが大切です。 モデルケースを考えて要領を掴むというのは、様々な問題に対応するための根本的な態度であり、とてつもない力があるということを実感してください。 例題は人と部屋でしたが、玉と箱も同じことです。 先ほどと違うのは、今度は空箱が許されています。 空箱が許されることによる勝手の違いを例題と比較しましょう。 なお、(1) の という問題が最も厄介です。 愚直に数え上げるしかないのですが、どうしても数式的に処理したいという方は 漸化式 という武器から迫る方法もあります。 ただ、数え上げる方が確実で早いため、別解とはせず、【総括】の中で触れておきました。 見た目は不定方程式の形をしていますが、 3つの箱に \(n\) 個の球を入れる。 この 3 つの箱にそれぞれ \(x\) 個 , \(y\) 個 , \(z\) 個 の球を入れる と考えると例題や類題のような 玉箱問題 となんら変わりません。 (2) が厄介で \(x \leq y \leq z\) という大小関係は言わば \((1個 \ , \ 2個 \ , \ 3個)\) はカウントするが、\((1個 \ , \ 3個 \ , \ 2個)\) はカウントしない みたいなことです。 つまり、玉も箱も区別なしということに他なりません。 類題1でも言いましたが、両方に区別がないのが一番厄介です。 この場合の対応については、経験がモノを言うところがありますが、基本方針は 区別がないから厄介 → じゃあ区別を与えよう という発想で考えていきます。 類題2は \(x\) , \(y\) , \(z\) が正の整数 だったため、玉箱問題で言えば、 空箱が許されない という状況でした。 最後の類題3のオチは「玉も箱も区別がない」という最も厄介なケースを空箱もありという状況で数えろという問題です。 玉も箱も区別がない場合は一般論でまとめることができないため、特殊なケースである \(n=6m\) の場合が与えられていますが、このあたりでひとまず着地したいと思います。 なお、考え方自体は類題2と同じであるため、類題3については略解であることをご了承ください。例題について
例題はこちら(再掲載)(画像をクリックするとPDFファイルで開きます。)
(1) について

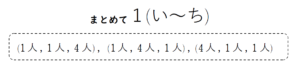
(2) について

(3) について
類題1について
類題1はこちら(再掲載)(画像をクリックするとPDFファイルで開きます。)
類題2について
類題2はこちら(再掲載)(画像をクリックするとPDFファイルで開きます。)
類題3(腕試し用類題)について
類題3【腕試し用類題】はこちら(再掲載)(画像をクリックするとPDFファイルで開きます。)




