例題はこちら（画像をクリックするとPDFファイルで開きます。）
類題１はこちら（画像をクリックするとPDFファイルで開きます。）
類題２はこちら（画像をクリックするとPDFファイルで開きます。）
求められない角度に対してどのようにアプローチするかを考える問題を扱います。
基本的には
等式を諦めて不等式を繋ぐ
という態度で臨みます。
今回扱う角度は具体的に口で言うことはできません。
「大体このぐらいの角度である」
というある意味ラフな気持ちが必要です。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む ひとまず絵をかいてみると というような感じでしょうか。 外接円同士は離れていてもいいのですが、最終的に配置できる「最大個数」を考えるので、ギリギリの接する場合で絵をかいています。 こうしてみると となりますから、 \(\sin{\theta}=2\sin{\displaystyle \frac{\theta}{2}}\cos{\displaystyle \frac{\theta}{2}}\) という２倍角公式により解決します。 \(\displaystyle \frac{\pi}{3} \lt \theta \lt \displaystyle \frac{\pi}{2}\) を示すわけですが、我々は 裸の角度 \(\theta\) に対してとれる態度は限られています。 そこで、\(\cos{ \ }\) の服を着せて \(\cos{\displaystyle \frac{\pi}{2}} \lt \cos{\theta} \lt \cos{\displaystyle \frac{\pi}{3}}\) を示すことにします。 \(0 \lt x \lt \pi\) において \(\cos{x}\) は単調減少であるため、中身の角度の比較がしやすいためです。 求める配置可能な最大数を \(n\) とします。 これを数式的にどう落とし込むかです。 (1) , (2) で考えていた \(\theta\) というのは言わば 円一個分が占める幅 みたいなものです。 幅と言うと語弊があるかもしれません。 この図においての円 \(Q\) の中心に人が立っていて、手を広げて 「あなたの占める範囲はここからここまでよ」 と言っているものだと思ってください。 そうなると、 \(n\theta \leq 2\pi \lt (n+1)\pi \) を満たすことになります。 要はこれを満たす最大の正の整数 \(n\) を求めればよいことになります。 (2) で得た \(\displaystyle \frac{\pi}{3} \lt \theta \lt \displaystyle \frac{\pi}{2}\) という関係式から \(2\pi \lt 6\theta\) で、\(6\theta\) は \(2\pi\) を超えてしまうため、\(n=6\) はアウトです。 一方、\(4\theta\) については \(4\theta \lt 2\pi\) と \(2\pi\) を超えないため、OKです。 そうなると、気になるのは \(n=5\) のときです。 つまり、\(5\theta\) と \(2\pi\) の大小、すなわち \(\theta\) と \(\displaystyle \frac{2\pi}{5}\) との大小 が決め手となります。 もちろん (2) 同様、\(\cos{ \ }\) の服を着せて \(\cos{\theta}\) と \(\cos{\displaystyle \frac{2\pi}{5}}\) の大小 を比較します。 つまり、\(\cos{\displaystyle \frac{2\pi}{5}}\) , すなわち \(\cos{72^{\circ}}\) の値を出す必要があるわけです。 これについては経験が必要で、 テーマ別演習：18°絡みの三角比 でしっかり解説しています。 例題同様 配置可能ということを角度に読み替えて立式する という力が要求されます。 ただし、角度の評価については例題よりは難し目です。 問題の設定は例題と似ていますが、オチが極限です。 半径 \(\displaystyle \frac{1}{n}\) の円を配置していくということで、\(a_{n}\) を具体的に出すことは困難です。 そこで、本人不在でも極限を出せる唯一の手法である はさみうちの原理 で仕留めるということを睨みます。 \(a_{n}\) をいかに挟むか ということに注力して考えていきましょう。例題について
例題はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
(1) について
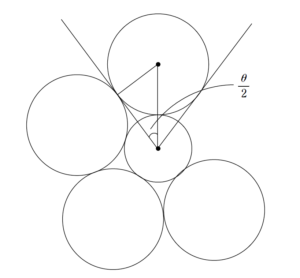
(2) について
(3) について
類題１について
類題１はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
類題２について
類題２はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）