例題はこちら(画像をクリックするとPDFファイルで開きます。)
通称「水の問題」と呼ばれている問題を扱います。
理解したうえで勘所をもっていないと、右往左往しかねませんし、解答を読んでも
聞けば分かるけど自力でできない
ということになりやすい問題です。
少しでも自力で解き進めるためにどういう意識をもって考えていくかということを少しでも持ち帰っていただければと思います。
(以下ネタバレ注意)
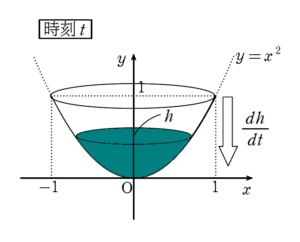
+ クリック(タップ)して続きを読む 今回の水の体積 \(V\) は時刻 \(t\) が変化するにつれ、刻一刻と変化していきます。 つまり、体積 \(V\) は時刻 \(t\) の関数として、気持ちの上で \(V(t)\) という意識をもっておきたいところです。 また、水面の高さ \(h\) も時刻 \(t\) に依存するため、時刻 \(t\) の関数です。 したがって水面の高さ \(h\) についても、時刻 \(t\) の関数という意味合いを込めて \(h(t)\) という意識をもっておきましょう。 容器の形が決まっていれば、水面の高さ \(h\) によって、水の体積が決まります。 つまり \(t\) が決まる → \(h\) が決まる → \(V\) が決まる という構造となります。 このような2段構造はいわば、合成関数です。 \(V=\displaystyle \int_{0}^{h}\pi x^{2} dy\) であり、\(y=x^{2}\) であることから $$\begin{eqnarray} というように、\(V\) が \(h\) で表せます。 上述の意識があれば \(\displaystyle \frac{dV}{dt}=\displaystyle \frac{dV}{dh} \cdot \displaystyle \frac{dh}{dt}\) という合成関数の微分法で仕留めることができるでしょう。 条件である \(\displaystyle \frac{dV}{dt}=-\sqrt{h}\) より \(-\sqrt{h}=\pi h \cdot \displaystyle \frac{dh}{dt}\) ということになり、 \(\displaystyle \frac{dh}{dt}=-\displaystyle \frac{1}{\pi \sqrt{h}}\) ということになります。 上述の \(h\) が時刻 \(t\) の関数という意識があれば、(1) で得た関係式は \(h'(t)=-\displaystyle \frac{1}{\pi \sqrt{h(t)}}\) という関係式で、「これを満たす \(h(t)\) はな~んだ?」という微分方程式です。 この微分方程式を解くことで \(h(t)\) を Get し、\(h(t)=0\) ( 水面の高さが 0 ) となる時刻 \(t\) を求めればよいことになります。 つまり、この微分方程式を捌くことが第2の山場ということです。 これについては \(h(t)^{\frac{1}{2}}h'(t)=-\displaystyle \frac{1}{\pi}\) として両辺 \(t\) で積分することで \(\displaystyle \int h(t)^{\frac{1}{2}}h'(t) dt=\displaystyle \int -\displaystyle \frac{1}{\pi} dt\) として、\(u=h(t)\) とおくことで \(\displaystyle \int u^{\frac{1}{2}} du=-\displaystyle \frac{1}{\pi} t+C_{1}\) すなわち \(\displaystyle \frac{2}{3} u^{\frac{3}{2}}=-\displaystyle \frac{1}{\pi} t+C\) という形で捌いていけます。 例題で頭の使い方などについて、一本筋が通っていると自力で結論まで行きつけるはずです。 例題の習得度を測るバロメーターとなる問題です。体積は時刻に依存する
水面の高さも時刻に依存する
容器の形が決まっていれば
本問を例に
V &=& \pi \displaystyle \int_{0}^{h}y dy \\
&=& \displaystyle \frac{1}{2} \pi h^{2}
\end{eqnarray}$$(2) について
類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)


