例題はこちら(画像をクリックするとPDFファイルで開きます。)
類題はこちら(画像をクリックするとPDFファイルで開きます。)
ニュートン法と呼ばれる「よりよい近似解」を求めるアルゴリズムについて考える問題です。
問題を解くこと自体は誘導がついているため、きちんとした基礎学力があれば無理なく進められるようにはなっています。
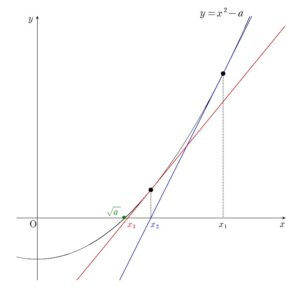
グラフ的に考えると、最後の極限の値は予測できますし、今回の数列 \(\{x_{n}\}\) がどのような数列であるかも理解できるでしょう。
ただ、グラフ的に考えるのはあくまでイメージであり、記述面においてはキッチリと式を用いて話を進めていきましょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む といったように、数列 \(\{x_{n}\}\) というのは 接線を引っ張り \(x\) 切片を拾っていく というように作られていく数列です。 こうしてみると、(2) のような単調減少性は納得いきますし、最後の極限値についても \(\displaystyle \lim_{n \to \infty}x_{n}=\sqrt{a}\) というのも即見えると思います。 ただし、式的にきちんと極限値を導出してほしいというのが出題者の趣旨でしょう。 そのためにわざわざ (3) を用意し、 はさみうちの原理で仕留めてくださいね というメッセージをご丁寧に出してくれています。 \((x_{n} \ , \ f(x_{n}))\) における接線の式を立て、それが \((x_{n+1} \ , \ 0)\) を通る ということを言えばよいでしょう。 \(x_{n}-x_{n+1}\) を計算すると \(x_{n}-x_{n+1}=\cdots=\displaystyle \frac {x_{n}^{2}-a}{2x_{n}}\) となります。 このことから \(x_{n} \gt \sqrt{a}\) を示すことができれば、右側、左側の不等式が同時に解決することになります。 この不等式証明については、(1) で数列 \(\{x_{n}\}\) についての漸化式が得られていることから、 数学的帰納法 で示そうとする態度が第一感です。 (2) で示した不等式により、絶対値は外れ、結局は \(x_{n+1}-\sqrt{a} \lt \displaystyle \frac {1}{2} (x_{n}-\sqrt{a})\) を示せばよいことになります。 これについては手なりに差をとって \(\displaystyle \frac {1}{2} (x_{n}-\sqrt{a})-(x_{n+1}-\sqrt{a})\) を計算していけば問題ありません。 (3) の不等式により \(|x_{n}-\sqrt{a}| \lt \displaystyle \frac {1}{2} |x_{n-1}-\sqrt{a}| \lt (\displaystyle \frac {1}{2})^{2} |x_{n-2}-\sqrt{a}| \lt \cdots \lt (\displaystyle \frac {1}{2})^{n-1} |x_{1}-\sqrt{a}|\) というように、番号を下げるごとに、\(\displaystyle \frac {1}{2}\) 倍されて上から押さえられていきます。 これにより \(0 \leq |x_{n}-\sqrt{a}| \lt (\displaystyle \frac {1}{2})^{n-1} |x_{1}-\sqrt{a}|\) を得て、はさみうちの原理から \(\displaystyle \lim_{n \to \infty}|x_{n}-\sqrt{a}|=0\) すなわち \(\displaystyle \lim_{n \to \infty} x_{n}=\sqrt{a}\) ということが言えます。 (1) で得られる \(x_{n+1}=\displaystyle \frac {{x_{n}}^{2}+a}{2x_{n}}\) という漸化式から、この数列 \(\{x_{n}\}\) は 初項と \(a\) が有理数なら、帰納的に全ての項が有理数 ということが言えます。 この有理数の数列 \(\{x_{n}\}\) は番号が上がれば上がるほど というわけです。 今回のような方法で近似解を求めていく手法を と言います。 例題の3乗根バージョンです。 例題のストーリーをしっかりと体に染み込ませていれば、目線がブレることはないでしょう。 なお、若干経験値が必要ですが、 縮小関数による漸化式によって定まる数列 というテーマに習熟していると、誘導に頼らずに (3) の不等式を得ることもできます。 これについては【総括】で触れておきました。 この話題にもしっかりと触れて有機的に結び付けたいということであれば 問題はこちら(画像をクリックするとPDFファイルで開きます。) 縮小関数による漸化式の極限という、難関大ではちょこちょこ出題されるテーマです。 もし、初見であれば、まずは初見でやってみて ... 続きを見る 問題はこちら(画像をクリックするとPDFファイルで開きます。) 縮小関数によって定まる漸化式によって定まる数列の極限を考える問題で、難関大を目指すにあたっては経験を積んでおきたい話題です。 本問は今回 ... 続きを見る を活用してください。例題について
例題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
イメージ
(1) について
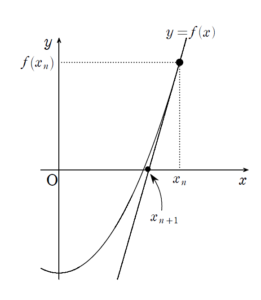
(2) について
(3) について
(4) について
ニュートン法について
類題について
類題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

参考縮小関数による漸化式の極限【関数によって定まる数列の極限】【1994年度 筑波大学】

参考2022年度 大阪大学 理系第4問【縮小関数による漸化式】


