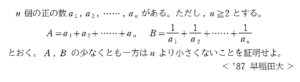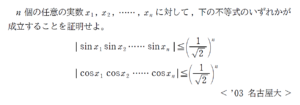例題はこちら(画像をクリックするとPDFファイルで開きます。)
\(A \geq n\) , \(B \geq n\) の少なくともどちらかは成り立つということを証明するという問題です。
方針面で「こうしてみようかな」という構想は出てくると思います。
解き終わってみると、ワンポイントレッスンのような問題に感じるでしょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む \(A \geq n\) または \(B \geq n\) が成り立つことを示すにあたり、少なくとも一方が成り立つことを直接証明するよりは \(A \lt n\) かつ \(B \lt n\) と仮定して矛盾を導く背理法が第一感でしょう。 この後ですが、辺々加えて \(A+B \lt 2n\) と見ると \((a_{1}+a_{2}+\cdots+a_{n})+(\displaystyle \frac {1}{a_{1}}+\displaystyle \frac {1}{a_{2}}+\cdots+\displaystyle \frac {1}{a_{n}}) \lt 2n\) です。 一方、相加平均・相乗平均の関係から \(a_{1}+\displaystyle \frac {1}{a_{1}} \geq \sqrt{a_{1}\cdot\displaystyle \frac {1}{a_{1}}}=2\) \(a_{2}+\displaystyle \frac {1}{a_{2}} \geq \sqrt{a_{2}\cdot\displaystyle \frac {1}{a_{2}}}=2\) \( \ \ \ \ \ \ \ \ \ \ \ \ \vdots\) \(a_{n}+\displaystyle \frac {1}{a_{n}} \geq \sqrt{a_{n}\cdot\displaystyle \frac {1}{a_{n}}}=2\) なので、辺々加えると \((a_{1}+a_{2}+\cdots+a_{n})+(\displaystyle \frac {1}{a_{1}}+\displaystyle \frac {1}{a_{2}}+\cdots+\displaystyle \frac {1}{a_{n}}) \geq 2n\) ということになり、矛盾します。 \(A+B \lt 2n\) と辺々加えると相加平均・相乗平均の関係が見えたわけですが、戦略的意図があって辺々加えたというよりも、「見えてしまった」という感覚に近いものがあると思います。 基本方針は例題と大きくは変わりません。 仮定してから、矛盾を導くまでの導線は例題よりは戦略的なものがありますが、それでも感覚的な部分もあることは否めないでしょう。 ある意味「こういうことをやってみよう」という力を磨くタイプの問題とも言えましょう。 三角関数の要素が加わった問題です。 例題の要素に加え、三角関数の基本的な運用力も試されます。 三角関数ならではの性質を活かした、様々な解法が考えられます。 解いておしまいでもいいですが、戯れるように色々考えてみるのも面白いですよ。第一感は背理法
類題について
類題1はこちら(画像をクリックするとPDFファイルで開きます。)
類題2はこちら(画像をクリックするとPDFファイルで開きます。)