問題はこちら(画像をクリックするとPDFファイルで開きます。)
見た目はベクトルの問題ですが、様々な解法が考えられます。
そのままベクトルで捌くのもいいですし、少し凝った解法で捌いてもよいでしょう。
正攻法に攻めても問題なく捌けるという点は試験場ではありがたいですね。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 見た目通りベクトルの問題として捌いていくことを考えてみます。 まず、3点 \(\mathrm{A}\) , \(\mathrm{B}\) , \(\mathrm{C}\) に注目し、正三角形 \(\mathrm{ABC}\) をベースに という図で考えたいと思います。 最初に大切なことなのですが、 ということ、つまり 形だけが問題である ということを看破しましょう。 サイズが関係ないのであれば、考えやすいサイズである一辺の長さが \(1\) の正三角形で考えて差し支えないでしょう。 線分 \(\mathrm{AP}\) , \(\mathrm{BC}\) の交点を \(\mathrm{Q}\) とすると \(\overrightarrow{\mathrm{AQ}}=(1-p) \overrightarrow{\mathrm{AB}}+p \overrightarrow{\mathrm{AC}}\) と、容易に \(\overrightarrow{\mathrm{AQ}}\) が Get できることから、 \(\overrightarrow{\mathrm{AP}}=k \overrightarrow{\mathrm{AQ}}\) というように、\(\overrightarrow{\mathrm{AQ}}\) を伸ばして \(\overrightarrow{\mathrm{AP}}\) を Get する方向性で考えていきます。 この「うまい」倍率 \(k\) をどのように求めるかですが、 と捉えて、 \(|\overrightarrow{\mathrm{OP}}|=半径\) という条件から \(k\) を特定します。 そのためには、\(\triangle{\mathrm{ABC}}\) の外接円半径が必要ですが、それについては正弦定理で調達すればよいでしょう。 この路線は【解1】で扱っています。 路線1同様、 \(\overrightarrow{\mathrm{AP}}=k \overrightarrow{\mathrm{AQ}}\) として、うまい倍率 \(k\) を特定していく方針を考えていきます。 この \(k\) を求める際の翻訳の仕方を幾何的に考えてみます。 点 \(\mathrm{P}\) がこの円上にあることの幾何的な翻訳は様々ありますが、 \(\mathrm{AQ}\) の長さが余弦定理で求まることを考えると、 方べきの定理 で \(\mathrm{QP}\) の長さが求められますから、欲しい倍率も求まることになります。 これについては【解2】で扱っています。 座標を設定するのも一つの手です。 ただし座標の場合、 のように、むやみやたらに貼り付けても自分で自分の首を絞めるだけです。 この例は少々極端ですが、 と貼り付ける人もいます。 別にこれでもできないことはないでしょうが、今回考える \(\overrightarrow{\mathrm{AP}}\) というのは 始点が \(\mathrm{A}\) です。 そう考えると、始点が原点にあった方が考えやすいでしょう。 つまり、 というように貼り付ける方が良さそうです。 また、冒頭述べたサイズについては、\(\mathrm{B}\) , \(\mathrm{C}\) の数値設定上無駄な分数を登場させなくて済むので、今度は一辺の長さが \(2\) となるように設定しておいた方がよさそうです。 路線1、路線2同様、点 \(\mathrm{P}\) がこの円の上にあることをどのように翻訳するかですが、座標でやる以上 円の方程式 を Get しようとするのが自然でしょうか。 \(\mathrm{A}\) , \(\mathrm{B}\) , \(\mathrm{C}\) という3点を通る円として考えてもいいですが、\(\triangle{\mathrm{ABC}}\) が正三角形なのであれば 外心と重心は一致する ということを考えれば、重心の座標を出せば、外心の座標も Get でき、中心の座標と半径が同時に手に入ります。 この路線は【解3】で扱っています。 今回のように、図形の問題は 幾何・座標・ベクトル・複素数平面 といった複数の解法選択が考えられます。 どの分野の問題として捌いていくかを考える訓練として 問題はこちら(画像をクリックするとPDFファイルで開きます。) 難関大の問題では図形を扱う際、どの分野で解き進めるかという選択を迫られることが多いです。 その分野として多いのが 図形を扱う代表的分野 ... 続きを見る 問題はこちら(画像をクリックするとPDFファイルで開きます。) 単位円上の4点 \(\mathrm{A}\) , \(\mathrm{B}\) , \(\mathrm{C}\) , \(\mat ... 続きを見る 問題はこちら(画像をクリックするとPDFファイルで開きます。) 二等分線上の点の位置ベクトルをどのように扱うかという問題です。 結局は 長さと方向をいかに準備するか ということにエネルギーを注ぐことに ... 続きを見る などもありますので、よければご活用ください。路線1:ベクトル
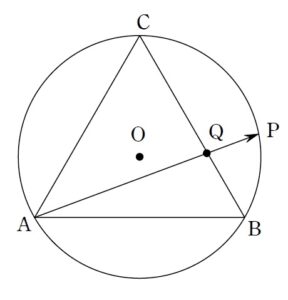
路線2:幾何
路線3:座標
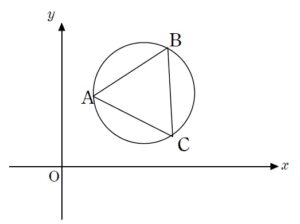
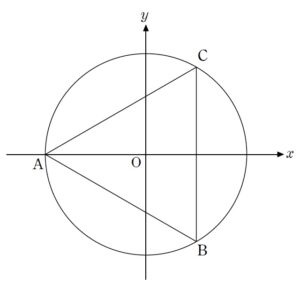
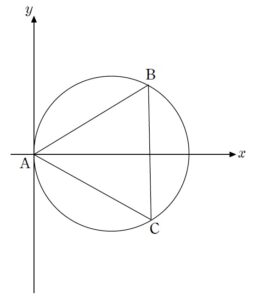
その他の問題

参考幾何・座標・ベクトル【別解の宝庫】【2002年度 京都大学】

参考22乗和と1乗和の解法選択【1993年度 一橋大学】

参考二等分線上の点の位置ベクトル【長さと方向をどう準備するか】【2004年度 京都大学】

