例題はこちら(画像をクリックするとPDFファイルで開きます。)
確率と極限の融合問題ですが、実質的にはまずは確率をきちんと計算できるかが要求されます。
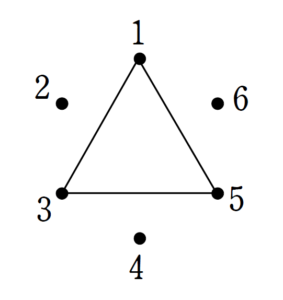
正六角形の頂点に印をうっていき、直角三角形ができるできないを考えるという、よくありそうな設定です。
ただ、意外と「ウッ」となる受験生は少なくないでしょう。
よくある設定のなかで、考えづらい要素を含むボディーブローのような問題です。
東大って結構そういう出題が特徴的だったりしますね。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む サイコロの目は毎回毎回1から6の目が出るわけで、当然同じ目が出て番号が重なっていくということがあり得ます。 番号が重なる重ならないという部分が鬱陶しさの一因になっているように思えます。 サイコロを3回投げて直角三角形ができる確率ということで、番号がダブっていることはあってはなりません。 なので、上述の番号が重なる重ならないという余計なことを心配する必要はないわけです。 直角三角形は により構成されるということが基本です。 \(p_{4}\) になると話が変わってきます。 この試行においては、基本的に ということが言えます。 相異なる4点印がつけば、その段階で直角三角形が存在することになります。 直角三角形ができないように印をうっていっても、4種類目には逃げ道がなくなるわけです。 つまり、何が言いたいかというと \(n\) が大きくなればなるほど、直角三角形じゃないことの方がレアケース ということです。 ある程度のレベルの確率の問題においては 直接計算 or 余事象の計算 という方針を迫られることが多いわけですが、今回はレアケースである「直角三角形ができない」という余事象を考えていく方が得策です。 今回考えるべき極限の式 \(\displaystyle \lim_{n \to \infty}\displaystyle \frac{1}{n} \log{(1-p_{n})}\) に含まれる \(1-p_{n}\) というのが、「直角三角形が存在しない確率」という余事象です。 もちろん、上述したように、レアケースである余事象に注目するという観点から見てもそうです。 なので、本問において余事象を考えるというのは極めて自然な判断です。 直角三角形が存在しないケースとしては という3つの可能性があり、場合分けしてそれぞれのケースを考えていきます。 例えばつけられている印の番号が3種類の場合は、三角形ができることは確定で、直角三角形でないというケースは というような 二等辺三角形となっているケース あるいは というように、 正三角形となっているケース が考えられます。 この後はそれぞれの場合で ポイント
モデルケースを考えてみて、同じ要領でその他のケースを考える という態度が有効です。 最後のオチが例題と同じです。 素材自体はサイコロを投げて出た目の積について考えていくという定番の話題です。 その場力が高い人は問題ないですが、この類題もある程度の経験という名の免疫をもっていないとアタフタしかねない問題で、やはりボディーブロー的な問題です。 場数を踏みたい方は 問題はこちら(画像をクリックするとPDFファイルで開きます。) 番号付きカードを取り出したり、サイコロを投げたりして番号の和や積を考える問題は沢山あります。 本問は典型的なテーマをベース ... 続きを見る もよかったらどうぞ。考えづらさの根元
(1) について
\(p_{3}\) について
\(p_{4}\) について
(2) について

類題について
類題はこちら(画像をクリックするとPDFファイルで開きます。)

参考カードの番号の積【直接考えるか余事象を考えるかの方針決定】【2009年度 千葉大学】


