例題はこちら（画像をクリックするとPDFファイルで開きます。）
類題はこちら（画像をクリックするとPDFファイルで開きます。）
ルートが絡んだ絶対不等式に関する問題です。
例題と類題を並べてみて、違いが分かるでしょうか。
例題、類題共に様々な解法がありますが、例題で学んだ解法をそのまま類題に適用しようとすると、方針によっては中々大変だったりします。
試験場で自分が選択する解法は一通りだと思いますが、普段の学習において別解を色々考えてみることや、比較検討することは大切なことです。
もちろん、今述べたことは基礎基本がしっかりと身についていることが前提で、基本があやふやな中別解を浴びてもかえって混乱するだけです。
ここでは、当たり前のことは当たり前にできるということを前提として話を進めます。
ひとまず例題を用いて、様々な解法を学んで、その学んだ解法が類題に活かせるかを考えてみてください。
もちろん、中には経験や観察力をもとにした閃きの要素が強い観賞用の解法もあると思います。
新たな解法を学んだとき
「あれ？これ以前やったあの問題でも使えないか？」
みたいな感じで使ってみる経験を積むことが大切です。
何度も言いますが、今回の例題で学ぶ解法の中には、類題では中々通用しない態度もあります。
解法の守備範囲的なことを意識してみてください。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む (1) については両辺正の値であることから \((\sqrt{a+b})^{2} \lt (\sqrt{a}+\sqrt{b})^{2}\) という２乗比較をすればよいという、定期考査レベルの問題です。 (2) が今回メインの話題です。 まずは考えやすくするために \(\displaystyle \frac{\sqrt{a}+\sqrt{b}}{\sqrt{a+b}} \leq k\) とみて、これが任意の正の実数 \(a\) , \(b\) に対して成立する \(k\) の条件について考えていきます。 左辺が色々な値をとるけど、全て \(k\) に負けてしまう ということですから、左辺の最大値に注目します。 一番強いやつが \(k\) に負けるなら、その他の連中も皆 \(k\) に負けるでしょ という戦国武将理論です。 左辺は一見、独立２変数関数です。 その最大値を考えるにあたり、１文字を固定して考える予選決勝法という手も十分考えられます。 ただ、ここは左辺の分母・分子を \(\sqrt{a}\) で割って \(\displaystyle \frac{\displaystyle \frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}}}{\displaystyle \frac{\sqrt{a+b}}{\sqrt{a}}} \leq k\) すなわち \(\displaystyle \frac{1+\sqrt{\displaystyle \frac{b}{a}}}{\sqrt{1+\displaystyle \frac{b}{a}}} \leq k\) と見て、\(\displaystyle \frac{b}{a}=t\) などとおくと \(\displaystyle \frac{1+\sqrt{t}}{\sqrt{1+t}} \leq k\) と１変数化できます。 これについては同次式に関する経験と、それを見落とさない観察力が必要です。 今回のこの路線について焦点を当てている記事として 問題はこちら（画像をクリックするとPDFファイルで開きます。） 特徴のある式についてはその個性を活かした扱い方をします。 もちろん、そんな個性のある式はそんなに沢山あるわけではありません ... 続きを見る などもありますので、適宜ご活用ください。 \(f(a+b)\) と \(f(a)+f(b)\) というような形の２数を比較する際に、\(f(x)\) の凸性に注目することもレベルが高くなってくると常套手段の一つです。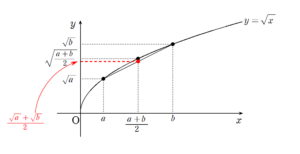 今回は \(f(x)=\sqrt{x}\) という関数が上に凸であることを利用していきます。 視覚化という態度は見たまんま終わるので、決まれば早いですが、反面見えるかどうかという部分にかかってきます。 今回は というイメージがもてるかどうかです。 独立２変数関数の最大最小を考えるにあたり、有名な絶対不等式を活用していくことも有力な手段の一つです。 それを意識していると コーシー・シュワルツの不等式 の活用も考えられます。 ただ、何かのセオリーに基づく戦略というよりは、経験や観察力寄りの発想にはなると思います。 \(\sqrt{a}=A\) , \(\sqrt{b}=B\) などとおいてやると \(A+B \leq k\sqrt{A^{2}+B^{2}}\) ということになります。 \(\sqrt{A^{2}+B^{2}}\) というのは \((0 \ , \ 0)\) と \((A \ , \ B)\) の距離という意味付けができますから、そこから崩すこともできます。 \(r\) は正の実数 , \(\theta\) を \(0 \lt \theta \lt \displaystyle \frac{\pi}{2}\) を満たす角として \(\sqrt{a}=r\cos{\theta}\) , \(\sqrt{b}=r\sin{\theta}\) と置き換えることによって、与えられた不等式は \(r(\cos{\theta}+\sin{\theta}) \leq kr\) すなわち \(\sqrt{2}\sin{(\theta+\displaystyle \frac{\pi}{4})} \leq k\) となり、左辺の最大値は \(\sqrt{2}\) と即分かってしまいます。 例題と違い、 対称性が崩れています。 これにより、例題で学んだ解法のうちいくつかはそのままでは通用しないということを実感してほしいと思います。 特に【方針２】の凸性の利用の方針を思いつくのが大変でした。 半分放棄しようかとも思いましたが、この話題を扱おうと決めた以上、最後は意地です（笑）例題について
例題はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
方針 1：絶対不等式としての処理と同次式の活用
参考同次式（斉次式）の扱いと絶対不等式としての処理【2016年度,1990年度 立命館大学】
方針２：凸性の利用
方針３：絶対不等式の活用
方針４：式の形を図形的に意味付けする
方針５：三角関数を利用した置き換え
類題について
類題はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）