折れ線問題の基本
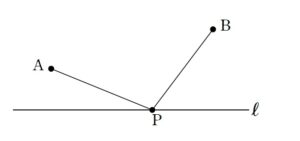
一番の基本問題は

のように定点 \(A\) , \(B\) と、直線 \(l\) 上を動く動点 \(P\) があり、\(AP+BP\) の最小値を求める問題です。
これについては

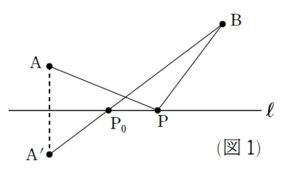
(図1)のように、対称点を考えて、\(AP=A'P\) となる \(A'\) を考えることが急所です。
これにより、\(AP+BP=A'P+BP\) となりますから、\(A'P+BP\) の最小値を考えることになります。
これについては移動軸を挟んでやることで、\(A'\) , \(P\) , \(B\) が一直線上に並ぶときが題意の折れ線が最小となるときであることが見えてきます。
【問題1】について
平面の問題【問題1】はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

動点が直線と円の2つになった場合、どのように考えればよいかという趣旨です。
基本的には、
折り返して一直線
という態度で倒すことになります。
頭ではどのように一直線上に並べばよいか、おぼろげながら分かるとは思います。
ただ、解く以上に言葉でそれを説明する難しさがあるでしょう。
そのあたりの記述をどうまとめるかが腕の見せ所です。
問題2について
空間の平面上を動く問題【問題2】はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

3次元バージョンです。
ただ、これも2次元バージョンと同じく基本的には
折り返して一直線
という態度です。
律儀に座標軸をとって正確な図を描こうと躍起になって時間を失っている受験生が多いのですが、

というように、分かりやすい(見やすい)図で考えれば十分です。
正確に描いた図で考えようが、上の図で考えようが、
立てる式は一緒
です。
もちろん、問題によっては正確に図を描くことが必要なこともありますし、正確に図を描くことで間違いに気が付けたというようなこともあったりします。
このあたりはケースバイケースなのですが、もし立てた式による結論と、自分の描いた図がリンクしていなかった場合、
「あ~、実際にはこうなっていたんだ」
といったように、「正しい状況は式が教えてくれる」ことが多いので、無駄に時間を取られないようにしましょう。
(もちろん計算ミスをしていないという前提の話です。)
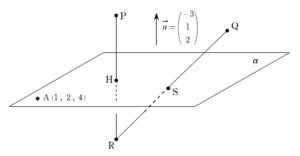
本問は、対称点を出したり、直線と平面の交点を出したりする際に
ベクトルの扱い
が問われます。
このあたりは、本問の話題以前の基本的なベクトルの運用力の問題になります。
問題3について
空間の直線上を動く問題【問題3】はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)

一番厄介なタイプです。

3次元空間においては対称点をとって一直線上に \(P\) をとろうと思っても

というように、直線 \(A'B\) と動点 \(P\) の移動軸が
ねじれの位置
となってしまい、交点をもたないのが一般的です。
ここをどう解決するかが腕の見せ所です。
なお、工夫を思いつかなかった場合、腕力で押し切ることも可能です。
その路線については、【総括】のあとの【エスケープ路線】で触れてあります。
問題1の解答はコチラ
問題2の解答はコチラ
問題3の解答はコチラ