問題はこちら(画像をクリックするとPDFファイルで開きます。)
極、極線という有名な構図があります。
その構図に関する有名事実をネタにした問題です。
工夫なしで立ち向かうとなると厳しい計算に襲われるかと思います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む とりあえずは座標を設定したいところです。 \(P\)\((p \ , \ 0)\) \((p \gt 1)\) などと設定するのが自然でしょうか。 \(P\) , \(Q\) , \(R\) , \(S\) は同一直線上にあるわけですが、その直線を \(l\) と呼びます。 \(l\) を立式することができれば円 \(C : x^{2}+y^{2}=1\) と連立すれば、交点 \(Q\) , \(R\) について捉えられますし、直線 \(AB\) と連立すれば、交点 \(S\) が捉えられます。 とは言え、直線 \(l\) を \(y=m (x-p)\) などと傾き \(m\) を設定すると ということでいばらの道に感じます。 与えられた状況を最大限生かそうと思うと ベクトル方程式による表現 直線 \(l\) 上の点 \(T\) が実数 \(t\) を用いて \(\overrightarrow{ OT }=\overrightarrow{ OP }+t \vec{d}\) と表現できる という、いわゆる「ベクトル方程式」で表現する方針が気持ちよくキマります。 (\(\vec{d}\) は直線 \(l\) の方向ベクトルです。) 円外の点 \(P\) から 2 本の接線を引き、その2接点を \(A\) , \(B\) とします。 (アルファベットは本問に合わせています。) このとき、この点 \(P\) を「極」、直線 \(AB\) を「極線」と言います。 \(P\) の座標を \((x_{0} \ , \ y_{0})\) とし、円の方程式を \(x^{2}+y^{2}=r^{2}\) としたときの極線 \(AB\) の方程式は \(x_{0}x+y_{0}y=r^{2}\) という式で与えられます。 なお、円の方程式が \((x-a)^{2}+(y-b)^{2}=r^{2}\) と、原点中心でない場合でも、極線の式は \((x_{0}-a)(x-a)+(y_{0}-b)(y-b)=r^{2}\) と、同じ要領で得ることができます。 調和点列 線分 \(AB\) を \(m \ : \ n\) に内分する点を \(P\) , 外分する点を \(Q\) とするとき 4 点 \(A\) , \(B\) , \(P\) , \(Q\) は調和点列である と言われます。 本問の結果は \(\displaystyle \frac{r_{1}+r_{2}}{r_{1}r_{2}}=\displaystyle \frac{2}{r}\) となり、これを整理すると \(r_{1}(r_{2}-r)=r_{2}(r-r_{1})\) すなわち \(PQ \cdot RS=PR \cdot QS\) を得るため、\(PQ \ : \ QS=PR \ : \ RS\) ということになり、 今回の 4 点 \(P\) , \(Q\) , \(R\) , \(S\) は調和点列である ということが言えます。 \(\displaystyle \frac{1}{r_{2}}\) , \(\displaystyle \frac{1}{r}\) , \(\displaystyle \frac{1}{r_{1}}\) という \(r_{1}\) , \(r\) , \(r_{2}\) の逆数が等差数列ということが「調和点列」と呼ばれる理由です。 \(y=f(x)\) のような \(x\) 座標と \(y\) 座標の関係を捉えることで、図形を表現する方法を 「直交座標表示」 といいます。 直交座標表示どうしを連立させて、交点を考えるということは多くの人は慣れていると思います。 それに対して、本問のように、 ベクトル方程式と直交座標表示を連立させて、交点を捉えるということは慣れている人は少ないでしょう。 「極と極線」やそれに関わる性質としての「調和点列に関するオチ」という事実的なことはもちろんのこと、ベクトル方程式を場面に応じてもちだして利用することも糧にしてもらえればと思います。まずは座標設定
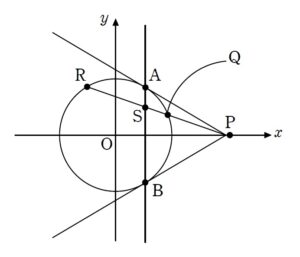
\(l\) を立式することができれば
\(PQ=r_{1}\) , \(PR=r_{2}\) , \(PS=r\) という距離を活かすために
極と極線
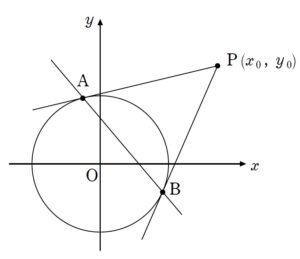
本問の結果は
本問の教訓

