問題はこちら(画像をクリックするとPDFファイルで開きます。)
微分積分に関する正誤判定の問題です。
- 「それらしい」主張に惑わされないこと。
- 勝手なMy Rule をふりかざさないこと。
ということに対する教訓にしてほしい問題です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む \(f'(x)=g'(x)\) とは \(\{f(x)-g(x)\}'=0\) ということです。 これより \(C\) を定数として \(f(x)-g(x)=C\) ということが言えると思います。 この \(C\) が \(C=0\) のときはもちろん \(f(x)=g(x)\) ですが、一般的に \(C=0\) とは限らないため、(1) の主張は誤りということになります。 \(\displaystyle \int_{0}^{1} f(x) dx=\displaystyle \int_{0}^{1} g(x) dx\) とは \(\displaystyle \int_{0}^{1} \{f(x)-g(x)\} dx=0 \cdots ①\) ということです。 もちろん、\(f(x)-g(x)=0\) というのも \(①\) を満たす場合の1つですが、 のような場合もあり得ることになります。 定積分が「符号付き面積」であることを考え、定積分の値が \(0\) というシチュエーションは、上の図のように正と負で打ち消しあうという場合を考えることになるわけです。 したがって、例えば \(f(x)-g(x)=2x-1\) となるような \(f(x)\) , \(g(x)\) が反例となることになります。 \(\displaystyle \int_{0}^{t} \{f(x)-g(x)\} dx=0\) が任意の \(t\) で成立するときを考えることになりますが、先ほどの面積的なイメージを考えると、常に打ち消しあって \(0\) ということは \(f(x)-g(x)\) が恒等的に \(0\) というとき以外ありえません。 つまり \(f(x)=g(x)\) が成り立ち、主張は正しいことになります。 \(\{f(x)-g(x)\}'=0\) のときを考えることになります。 このときは (1) 同様、\(C\) を定数として \(f(x)-g(x)=C\) ということになります。 加えて \(\displaystyle \int_{0}^{1} \{f(x)-g(x)\} dx=0\) すなわち \(\displaystyle \int_{0}^{1} C dx=0\) という条件から \(C=0\) ということになります。 これより、 \(f(x)-g(x)=0\) すなわち \(f(x)=g(x)\) が成り立つことが言え、主張は正しいことになります。 \(\displaystyle \int_{0}^{t} \{f(x)-g(x)\} dx \geq 0 \cdots ②\) が \(t \geq 0\) なる任意の \(t\) で成立するときを考えることになります。 もちろん、\(x \geq 0\) の範囲で常に \(f(x)-g(x) \geq 0\) が成立していれば、文句はないですが、 のように、負の面積部分が少ししかなく、正の面積を打ち消すに及ばない場合、\(②\) を満たすことになり、これが反例ということになります。 \(\{f(x)-g(x)\}' \geq 0\) すなわち \(f(x)-g(x)\) が単調増加 であるときを考えることになります。 例えば \(f(x)-g(x)=x+1\) のようなときを考えてみます。 こうなるような \(f(x)\) , \(g(x)\) として などがあります。 任意の \(x\) に対して \(f'(x)=2\) , \(g'(x)=1\) ですから \(f'(x) \geq g'(x)\) ですが、 常に \(f(x) \geq g(x)\) とは限らないため、主張は誤りで、上の \(f(x)\) , \(g(x)\) が反例ということになります。(1) について
(2) について
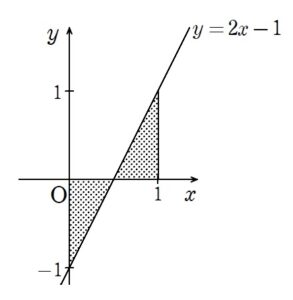
(3) について
(4) について
(5) について
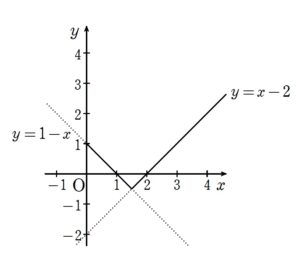
(6) について

