問題1はこちら(画像をクリックするとPDFファイルで開きます。)
問題2はこちら(画像をクリックするとPDFファイルで開きます。)
問題3はこちら(画像をクリックするとPDFファイルで開きます。)
群数列の基本とその運用に関して確認し、足固めする問題です。
基本的に群数列は「めんどくさい」と思う人も多いです。
確かに
「何?何?何?ちょっと待て、え~っと」
と、設定が複雑な問題も多々あります。
群数列の目の付け所や話の進め方は基本的に一本道です。
今回は極力設定がシンプルで、その目の付け所や話の進め方に集中できる例題として良問を3題扱います。
加えて、群数列はその急所を「言葉でまとめにくい」です。
少しでも群数列の「勘所」を汎用性のある形でまとめることを目標にしたいと思います。
群数列の基本
群数列の基本は
群数列でやるべきこと
ターゲットの住所を特定する
ということです。
群数列の住所とは
「ターゲットが第何群の何番目か」
ということです。
個数と添え字のリンク
一つインストールしておきたい「当たり前」のことがあります。
それは
\(\overbrace{a_{1} \ , \ a_{2} \ , \ \cdots \ , \ a_{N}}^{N個}\)
と
「そこまでに \(N\) 個あるから、最後が \(a_{N}\) と呼ばれる」
ということです。
つまり、そこまでの「個数」と「添え字」はリンクするわけです。
住所を特定するためのイメージ
\(a_{n}\) が第 \(M\) 群の \(N\) 番目にあるときに、どのような立式ができるかを把握するために
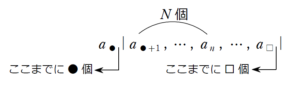
というイメージをもちます。
これにより
$$\begin{eqnarray}
\left\{
\begin{array}{l}
● \lt n \leq □ \\
●+N=n
\end{array}
\right.
\end{eqnarray}$$
という式が立式できるわけです。
この \(●\) や \(□\) というのは「各群の末項までの個数」です。
つまり一般的に
第 \(k\) 群の末項までの項数
を把握しておく必要があるわけです。
群数列でよく訊かれること
訊かれることが多いのは
- ターゲットの住所や正体
- ターゲットまでの和
です。
これらを求めるための基本的な姿勢は
基本姿勢
群ごとに数えていき(加えていき)、はみ出た部分は手作業
という姿勢です。
あとは具体的な問題を通じて、どういう要領なのかを体得していきましょう。
問題1について
問題1はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
100メートル先から見ても群数列の問題と分かる「The 例題」的な問題です。
上記のイメージに基づいた立式を通じて、各ターゲットの住所を考えていきます。
問題2について
問題2はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
二項係数を並べた数列ですが、
\({}_k \mathrm{ C }_0\) , \({}_k \mathrm{ C }_1\) , \(\cdots\) , \({}_k \mathrm{ C }_k\)
を第 \(k\) 群とするような群数列を考えます。
基本方針は大きくは変わりません。
最後の和を考える際ですが、「二項係数の和」について考えることになります。
これは「シグマ計算」という別テーマの話題です。
問題3について
問題3はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
上記2題に比べれば、群数列が前面に出ている問題文ではありません。
ただ、実験してみると
\(\sqrt{1}=1\)
\(\sqrt{2}=1.41\cdots\)
\(\sqrt{3}=1.73\cdots\)
\(\sqrt{4}=2\)
\(\sqrt{5}=2.23\cdots\)
なので、
\(a_{1}=1\) , \(a_{2}=1\) , \(a_{3}=2\) , \(a_{4}=2\) , \(a_{5}=2\)
のように、同じ数字がある程度続くような数列です。
こうしてみると群数列として考えることが見えてきます。
また、この「ある程度」というのが具体的に何個続くのかを式として立式したいという思いが出てくると思います。
(1) でそれが訊かれているわけですが、どちらかと言うと自分で調べたいことでしょう。
また、今回は「\(\sqrt{n}\) に最も近い整数を \(a_{n}\)」という設定でしたが、
\(a_{n}=[\sqrt{n}]\) と、小数部分を切り捨て、\(\sqrt{n}\) の整数部分という設定の問題もあります。



