例題はこちら(画像をクリックするとPDFファイルで開きます。)
メネラウスの定理の空間版ともいえる内容の証明を考える問題です。
一応、ベクトルでゴリ押しすることもできますが、そちらについては【復習用問題】の【総括】で扱うことにします。
ここでは平面版のメネラウスの定理の拡張を前面に出した幾何的な路線をメインの路線として考えてみます。
(以下ネタバレ注意)
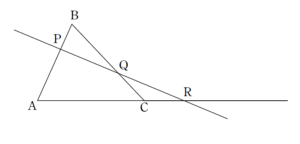
+ クリック(タップ)して続きを読む というように、 \(\triangle{\mathrm{ABC}}\) を、直線 \(l\) で ぶった切る というイメージを持ってください。 ぶった切ったときの、3角形の辺(または延長線)の切り口の交点を図のように \(\mathrm{P}\) , \(\mathrm{Q}\) , \(\mathrm{R}\) とすると \(\displaystyle \frac{\mathrm{AP}}{\mathrm{PB}} \cdot \displaystyle \frac{\mathrm{BQ}}{\mathrm{QC}} \cdot \displaystyle \frac{\mathrm{CR}}{\mathrm{RA}}\) というように、ある頂点(例では \(\mathrm{A}\) )からスタートし、 と頂点と交点を交互に踏みながら1周したときに、比率の積が \(1\) となるという定理がメネラウスの定理です。 そう考えると 四面体 \(\mathrm{ABCD}\) を平面でぶった切ったときの切り口の交点 \(\mathrm{P}\) , \(\mathrm{Q}\) , \(\mathrm{R}\) , \(\mathrm{S}\) に対して \(\displaystyle \frac{\mathrm{AP}}{\mathrm{PB}} \cdot \displaystyle \frac{\mathrm{BQ}}{\mathrm{QC}} \cdot \displaystyle \frac{\mathrm{CR}}{\mathrm{RD}} \cdot \displaystyle \frac{\mathrm{DS}}{\mathrm{SA}}=1\) という今回の主張は という、まさにメネラウスの定理であり、空間版メネラウスの定理と言えましょう。 実は (2) の設定の方が幾何的にはありがたい構図です。 というように、平面 \(\mathrm{ABC}\) 上の直線 \(\mathrm{PQ}\) と平面 \(\mathrm{ACD}\) 上の直線 \(\mathrm{RS}\) の交点 \(\mathrm{T}\) は ということになります。 この2平面上の2つの三角形 \(\triangle{\mathrm{ABC}}\) , \(\triangle{\mathrm{ACD}}\) に対して、それぞれメネラウスの定理を用いてみてください。 気持ちよく題意の主張が成り立つことが浮き上がってきます。 2直線\(\mathrm{PQ}\) , \(\mathrm{RS}\) が平行のときだと、この2直線が交点をもたないため、上の議論ができません。 潔くベクトルを用いてゴリゴリ計算していきます。 内容は例題と同じです。 勉強のため、例題では幾何的な路線を前面に出しましたが、ベクトルを用いて最初から最後まで押し通すものをこちらの【総括】で触れておきました。平面版のメネラウスの定理の主張
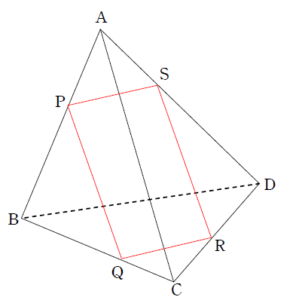
(2) の方が実はありがたい
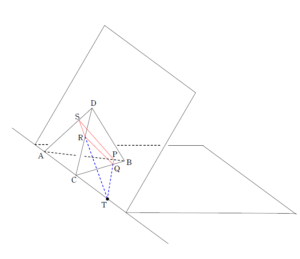
(1) について
復習用問題について
復習用問題はこちら(画像をクリックするとPDFファイルで開きます。)


