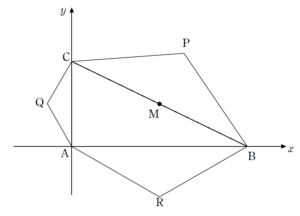
問題はこちら(画像をクリックするとPDFファイルで開きます。)
直角三角形の外側に作る二等辺三角形によって正三角形ができるという話題です。
どんな直角三角形に対しても、外側に頂角 \(120^{\circ}\) の二等辺三角形を配置することで正三角形が作れるという事実は面白いですね。
本問は誘導がついていましたが、誘導があると面白みが薄れるため、今回は誘導設問はカットしました。
ノーヒントで取り組んでみてください。
ノーヒントでも無理なく捌ききれるレベルだと思います。
(以下ネタバレ注意)
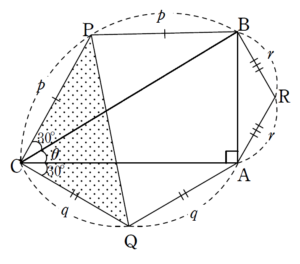
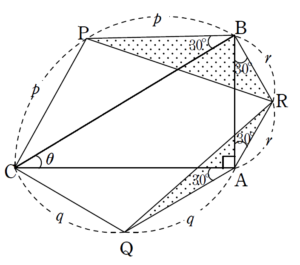
+ クリック(タップ)して続きを読む ひとまず、構図を把握し、長さを設定するところからスタートします。 図のように $$\begin{eqnarray} と、直角三角形の3辺の長さを設定します。 また、二等辺三角形の二等辺の長さについて $$\begin{eqnarray} と設定します。 これら \(a\) , \(b\) , \(c\) と \(p\) , \(q\) , \(r\) はもちろん従属関係で、頂角 \(120^{\circ}\) の二等辺三角形であることから $$\begin{eqnarray} という関係式を得ます。 ただ、どちらかと言えば、 \(a\) , \(b\) , \(c\) が決まって \(p\) , \(q\) , \(r\) が決まる、すなわち というように見るのが自然かなと思います。 (順番的にも直角三角形を描いて、それに応じて二等辺三角形を作るわけですから) そこで、 $$\begin{eqnarray} として見ます。 \(\triangle{\mathrm{PQR}}\) が正三角形であることを示すには \(\mathrm{PQ}=\mathrm{QR}=\mathrm{RP}\) と、3辺の長さが等しいことを目指すのがドストレートな方針です。 そこで、この3辺 \(\mathrm{PQ}\) , \(\mathrm{QR}\) , \(\mathrm{RP}\) の長さを計算していきます。 線分 \(\mathrm{PQ}\) の長さを計算したいので、線分 \(\mathrm{PQ}\) を含む \(\triangle{\mathrm{PCQ}}\) に注目します。 \(\angle{\mathrm{ACB}}=\theta\) とおき、\(\triangle{\mathrm{PCQ}}\) で余弦定理を用いると \(\mathrm{PQ}^{2}=p^{2}+q^{2}-2pq\cos{(\theta+60^{\circ})}\) という式が立ちます。 \(p\) , \(q\) については \(a\) , \(b\) で表せます。 加法定理でバラした際に \(\sin{\theta}\) , \(\cos{\theta}\) が必要になりますが、直角三角形の定義から \(\sin{\theta}=\displaystyle \frac{c}{a}\) , \(\cos{\theta}=\displaystyle \frac{b}{a}\) と言えますから、\(\mathrm{PQ}^{2}\) が \(a\) , \(b\) , \(c\) で表せることになります。 詳しい計算結果は解答 PDF をご覧ください。 \(\mathrm{PQ}^{2}=\displaystyle \frac{1}{3}(a^{2}+\sqrt{3}bc)\) となります。 \(\mathrm{QR}\) , \(\mathrm{RP}\) についても同様に \(\triangle{\mathrm{AQR}}\) , \(\triangle{\mathrm{BRP}}\) に注目し、余弦定理を経由し \(\mathrm{QR}^{2}\) , \(\mathrm{RP}^{2}\) を計算していきます。 計算の方向性としては という着地点を睨みながら計算していきます。 直角ということを活かして というように、座標設定してしまうというのも一つの手です。 \(\mathrm{Q}\) , \(\mathrm{R}\) の座標はそこまで苦労することなく \(\mathrm{Q}\) \((-\displaystyle \frac{c}{2\sqrt{3}} \ , \ \displaystyle \frac{c}{2})\) \(\mathrm{R}\) \((\displaystyle \frac{b}{2} \ , \ -\displaystyle \frac{b}{2\sqrt{3}})\) と得られます。 問題は \(\mathrm{P}\) の座標で、こいつをいかに Get するかというところでしょう。 結局 \(\overrightarrow{\mathrm{AP}}\) が欲しいわけですが、線分 \(\mathrm{BC}\) の中点を \(\mathrm{M}\) として \(\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{AM}}+\overrightarrow{\mathrm{MP}}\) というように見ます。 したがって、最終的には \(\overrightarrow{\mathrm{MP}}\) をどのように出すのかという話になります。 これについては【解2】【解3】として 【解2】:直線 \(\mathrm{BC}\) の法線ベクトルを経由して出す路線 【解3】:\(\overrightarrow{\mathrm{BC}}\) に垂直なベクトルを経由して出す路線 という路線で捌いています。 本質的にはどちらも大差ありませんが、一応勉強のために触れておきました。構図の把握と、長さの設定
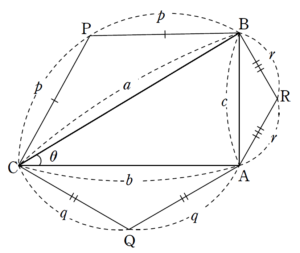
\left\{
\begin{array}{l}
\mathrm{BC}=a\\
\mathrm{CA}=b\\
\mathrm{AB}=c
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
\mathrm{PB}=\mathrm{PC}=p\\
\mathrm{QC}=\mathrm{QA}=q\\
\mathrm{RA}=\mathrm{RB}=r
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
a=2p\sin{60}^{\circ}=\sqrt{3}p\\
b=2q\sin{60}^{\circ}=\sqrt{3}q\\
c=2r\sin{60}^{\circ}=\sqrt{3}r
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
p=\displaystyle \frac{a}{\sqrt{3}} \\
q=\displaystyle \frac{b}{\sqrt{3}} \\
r=\displaystyle \frac{c}{\sqrt{3}}
\end{array}
\right.
\end{eqnarray}$$正三角形であることを示すには
\(\mathrm{PQ}\) の長さについて
\(\mathrm{QR}\) , \(\mathrm{RP}\) の長さについて
別解について