問題はこちら（画像をクリックするとPDFファイルで開きます。）
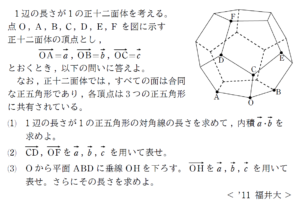
正十二面体に関する位置ベクトルについての問題です。
必然的に正五角形に関する扱いが求められます。
空間ベクトルの問題においては、正四面体などの簡単な立体は扱ったこともあるでしょうが、正十二面体となるとキッチリと地力の差が出るでしょう。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む 正五角形に含まれる黄金三角形の黄金分割によって、正五角形の対角線の長さを求めていきます。 これらの用語が初耳だという方は テーマ別演習：18°絡みの三角比 で詳しく解説していますので、参考にしてください。 $$\begin{eqnarray} なので、結局は \(\cos{72^{\circ}}\) が分かれば解決です。 なお、対角線の長さを \(x\) などと文字で置いておくと、その後も使いまわせるので便利です。 考えやすくするために、適切に平面を取り出して考えていきます。 \(\overrightarrow{\mathrm{CD}}\) については \(\mathrm{O}\) , \(\mathrm{A}\) , \(\mathrm{C}\) , \(\mathrm{D}\) を含む正五角形を取り出して考えます。 という構図となります。 \(\overrightarrow{\mathrm{AD}}=x\overrightarrow{\mathrm{OC}}\) と見るのが急所です。 \(\overrightarrow{\mathrm{OF}}\) については \(\overrightarrow{\mathrm{OF}}=\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CF}}\) と繋いでいきます。 この \(\overrightarrow{\mathrm{CF}}\) というのは、ある意味 正五角形の対角線に向かうベクトル ということで、前半のノウハウが使えます。 そのためには、\(\overrightarrow{\mathrm{CE}}\) , もっと言うと \(\overrightarrow{\mathrm{OE}}\) が必要になります。 必要に応じて正五角形を取り出して考えていきましょう。 平面 \(\mathrm{ABD}\) 上の点 \(\mathrm{H}\) については 共面条件 \(\overrightarrow{\mathrm{OH}}=\alpha \overrightarrow{\mathrm{OA}}+\beta \overrightarrow{\mathrm{OB}}+(1-\alpha-\beta)\overrightarrow{\mathrm{OD}}\) と表すことができます。 \(\overrightarrow{\mathrm{OH}}\) は 平面 \(\mathrm{ABD}\) と垂直なので、平面 \(\mathrm{ABD}\) 上の２本のベクトル \(\overrightarrow{\mathrm{AB}}\) , \(\overrightarrow{\mathrm{AD}}\) と垂直です。 式的には $$\begin{eqnarray} ということになります。 \(\alpha\) , \(\beta\) という未知数２つに対して、条件式も２つありますから、勝負ありです。 これにより、\(\overrightarrow{\mathrm{OH}}\) が \(\vec{a}\) , \(\vec{b}\) , \(\vec{c}\) で表せ、これらの大きさや内積は手中にあるため \(|\overrightarrow{\mathrm{OH}}|^{2}\) という２乗計算を経由して長さを求めていけます。(1) について
\vec{a} \cdot \vec{b}&=& |\vec{a}||\vec{b}|\cos{108^{\circ}} \\
&=& -\cos{72^{\circ}}
\end{eqnarray}$$(2) について
\(\overrightarrow{\mathrm{CD}}\) について
\(\overrightarrow{\mathrm{OF}}\) について
(3) について
\left\{
\begin{array}{l}
\overrightarrow{\mathrm{OH}} \cdot \overrightarrow{\mathrm{AB}} = 0 \\
\overrightarrow{\mathrm{OH}} \cdot \overrightarrow{\mathrm{AD}} = 0
\end{array}
\right.
\end{eqnarray}$$