例題はこちら（画像をクリックするとPDFファイルで開きます。）
類題１はこちら（画像をクリックするとPDFファイルで開きます。）
類題２はこちら（画像をクリックするとPDFファイルで開きます。）
極大値と極小値の和と差について考える問題です。
工夫の余地もあるトピックスなので、できればそちらも自分の血となり肉となる状態を目指していきたいところです。
ただ、緊張した試験場において何かの拍子でとんでしまっても、真正面から解ききるだけの地力はつけておく必要があります。
要するに欲張って色々勉強したいトピックスということです。
（以下ネタバレ注意）
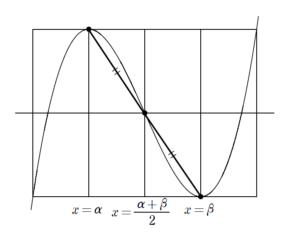
+ クリック（タップ）して続きを読む 本問で言えば、(2) が今回のトピックスである極大値と極小値の和です。 というように、\(\alpha\) , \(\beta\) に関する対称式として表せます。 基本対称式である \(\alpha+\beta\) , \(\alpha \beta\) については、\(\alpha\) , \(\beta\) の元々の出どころである \(f'(x)=0\) という２次方程式による、 解と係数の関係 から導出することになります。 という３次関数の変曲点に関する点対称性を認めれば、変曲点は \((\displaystyle \frac{\alpha+\beta}{2} \ , \ \displaystyle \frac{f(\alpha)+f(\beta)}{2})\) であり、\(y\) 座標に注目すれば \(\displaystyle \frac{f(\alpha)+f(\beta)}{2}\) は変曲点の \(y\) 座標 ということになります。 本問に限った話ではないですが、上のグラフの特徴である、３次関数のグラフの等間隔性もきちんと押さえておきましょう。 基本
３次関数は８畳１間に住んでいる という言葉もあります。 (3) が今回話題の極大値と極小値の差についての設問です。 \(x=s\) で極大値 \(f(s)\) , \(x=t\) で極小値 \(f(t)\) をもつとすると \(f(s)-f(t)=(s^{3}-t^{3})-3 (s^{2}-t^{2})+k(s-t)\) となります。 これについては、将来的に \(s-t\) で括れることが見込まれます。 (2) の結果から \(s-t\) を得ることは容易です。 極大値と極小値の差については \(f(s)-f(t)=\left[ f(x) \right]_t^s=\displaystyle \int_{t}^{s}f'(x)dx\) と定積分を逆に見る方向で処理するという方法が有名です。 被積分関数 \(f'(x)=3x^{2}-6x+k\) について \(f'(x)=0\) の異なる２つの実数解が \(s\) , \(t\) であるため、 \(f(s)-f(t)=\displaystyle \int_{t}^{s} 3 (x-s)(x-t) dx\) となり、ここからは \(\displaystyle \frac{1}{6}\) 公式で処理できます。 注意
\(f'(x)\) の最高次の係数である３に注意しましょう。 経験がないと中々できない方針ですが、破壊力は抜群です。 極大値と極小値の差についての類題です。 類題１を学習していれば、真正面から切り伏せても、工夫してもよいでしょう。 方針面においては煮るなり焼くなりという感じです。 ただ、それにしてもまともにやりだすとツライものがあるでしょう。 類題１とはまた別の工夫の余地もあります。 その工夫は今回のトピックスに限らず、汎用性の高い工夫なので、そこも今後の糧としてもらえればと思います。極大値と極小値の和について
例題はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
真正面からの計算
工夫の余地
極大値と極小値の差について
類題１はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
真正面からの計算
工夫の余地
類題２について
類題２はこちら（再掲載）（画像をクリックするとPDFファイルで開きます。）