問題はこちら(画像をクリックするとPDFファイルで開きます。)
「カルキン・ウィルフ・ツリー」と呼ばれる有理数の生成に関する不思議な樹形図の問題です。
この年の大阪大学のセットの中で最難問とも名高い問題で、機械的なマニュアル君は手も足も出ない可能性があります。
鋭い人は「当たり前じゃん」とさえ思える内容なのですが、どのように言語化するべきなのかも難しいでしょう。
数学でぶん殴りたいという受験生以外の人にとっては、合否に直結する問題ではないかもしれませんが、普段の学習においてはこういう問題に対して粘り強く考える姿勢はもっておきたいところです。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 既約分数 \(\displaystyle \frac{p}{q}\) から生成される2つの分数 \(\displaystyle \frac{p}{p+q}\) , \(\displaystyle \frac{p+q}{q}\) というものがどちらも既約分数であるということが言えれば、スタートの \(\displaystyle \frac{1}{1}\) が既約分数であることから帰納的にこの樹形図に現れる全ての分数が既約分数であることになります。 したがって示すべきは、 \(p \ , \ q\) が互いに素であるとき である。 ということです。 これについては、互いに素ということが \(2\) 以上の公約数をもたない という否定的な命題であることから、背理法を用いて捌きたくなるでしょう。 どんな有理数にも辿り着けるか? というような「下へ下へと下っていく」意識よりも 例えば \(\displaystyle \frac{3}{5}\) ってどこから来るんだ? という 「上へ上へと登っていく」意識 をもてるとしめたものです。 上へ遡ろうとするとなると \(p \gt q\) のとき \(\displaystyle \frac{p}{q} \to \displaystyle \frac{p-q}{q}\) \(q \gt p\) のとき \(\displaystyle \frac{p}{q} \to \displaystyle \frac{p}{q-p}\) という作業です。 要するに 分母・分子の大きい方から小さい方を引く という作業を繰り返すことになります。 例えば \(\displaystyle \frac{3}{5}\) の場合を考えてみましょう。 \(\displaystyle \frac{3}{5} \to \displaystyle \frac{3}{2} \to \displaystyle \frac{1}{2}\) ということになります。 これは という遡る「ルート」に対応することになります。 このように、\(\displaystyle \frac{p}{q}\) からこの上へ遡る作業をすること、すなわち 分母・分子の大きい方から小さい方を引く という作業をすれば、分母、分子は段々と小さくなっていきますから、やがて \(\displaystyle \frac{1}{r}\) , \(\displaystyle \frac{r}{1}\) のいずれかの形に帰着することになります。 この \(\displaystyle \frac{1}{r}\) , \(\displaystyle \frac{r}{1}\) は樹形図の右端、左端に必ずいます。 つまり、任意の正の有理数に辿り着くルートが存在することになるわけで、証明完了ということになります。 \(\displaystyle \frac{p}{q}\) から先ほどの上へ遡るという作業である 分母・分子の大きい方から小さい方を引く ということを繰り返し、 \(\displaystyle \frac{1}{r}\) , \(\displaystyle \frac{r}{1}\) まで辿り着く計算過程 (樹形図のルート) は一意的なものです。 もし、\(\displaystyle \frac{p}{q}\) が2カ所以上に現れるとなると、このルートが異なることになってしまい、矛盾してしまいます。 したがって、背理法により\(\displaystyle \frac{p}{q}\) は2カ所以上に現れることはなく、ダブることはないことが示されました。 ここまでくれば、\(\displaystyle \frac{19}{44}\) も上へ遡っていきたくなるでしょう。 \(\displaystyle \frac{19}{44}\) から上へ遡っていくと ということになりますから、\(\displaystyle \frac{1}{6}\) を基準にしたツリーを書けば、 というように、原始的に追っていくことができます。 本問の (2) , (3) の結果から、この樹形図(カルキン・ウィルフ・ツリー)に現れる有理数は 漏れなく、重複なく 現れていることになります。 これにより、正の有理数の集合が 可算集合である ということが言えることになります。 可算集合というのは、硬く言えば 要素の1つ1つが、自然数と1対1に対応する集合 というもので、誤解を恐れずざっくり言えば 要素を「い~ち、にぃ~、\(\cdots\)」と数えられる集合 というものです。 このことについては【総括】でちょっとだけ触れました。(1) について
(2) について
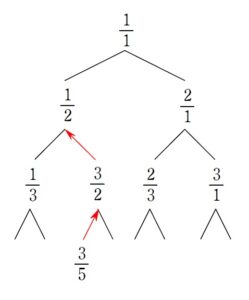
(3) について
(4) について
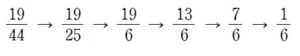
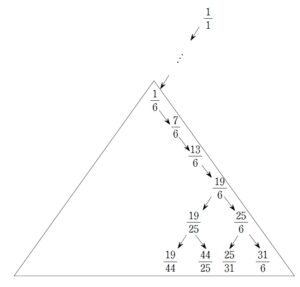
有理数の可算性

