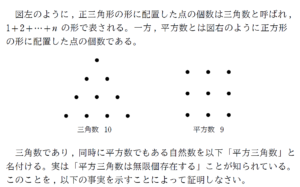
問題はこちら(画像をクリックするとPDFファイルで開きます。)
三角数かつ平方数となる数について考える問題です。
例えば、\(36\) という数は
- \(36=6^{2}\)
- \(36=1+2+3+4+5+6+7+8\)
と平方数でありながら、三角数でもあります。
このようなものが無数に存在することを示すのがオチです。
この「平方三角数」を作成する際に、
\(x^{2}-2y^{2}=1\)
というペル方程式が関わってくるあたりが面白く、興味深いですね。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 基本的な偶奇に関する問題です。 \(a^{2}=2b^{2}+1\) と、移項すれば ということが言えます。 ここから \(a\) も奇数ということになります。 これについては自明といってもよいでしょうが、証明問題なので記述では \(a\) が偶数ならば \(a^{2}\) が偶数である という命題の対偶を考えることを記述しておけばよいでしょう。 \(b\) が偶数であることについて 今度は \(b\) を含む部分に注目し \(2b^{2}=a^{2}-1\) と移項してやります。 これにより \(2b^{2}=(a+1)(a-1)\) で、\(a+1\) , \(a-1\) がともに偶数であることから ということになり、\(b^{2}\) が偶数となります。 したがって、\(b\) も偶数ということが言えます。 \(x^{2}-2y^{2}=1\) というペル方程式の解 \((x \ , \ y)=(a \ , \ b)\) が得られたとき、 と表すことにより \((2n+1)^{2}-8m^{2}=1\) という関係式を得ます。 これを整理すると \(m^{2}=\displaystyle \frac{n(n+1)}{2}\) を得ます。 まず、\(m^{2}\) が平方数であることはいいでしょう。 そして、 \(\displaystyle \frac{n(n+1)}{2}=1+2+\cdots+n\) ということを考えると \(m^{2}=1+2+\cdots+n\) ということになり、\(m^{2}\) が三角数でもあることが言えます。 つまり、\(x^{2}-2y^{2}=1\) というペル方程式の解 \((x \ , \ y)=(a \ , \ b)\) が得られたとき、(1) から \(b\) が偶数であることが言え、 \(b=2m\) と表したときの \(m^{2}\) が題意の平方三角数ということになります。 ペル方程式の自然数解から平方三角数が作れることが分かりましたから、あとはペル方程式の自然数解をどのように得るかということになります。 今回は手の内を晒した証明問題であるため、方針自体は迷う余地がありません。 今回の数列 \(\{a_{n}\}\) , \(\{b_{n}\}\) について漸化式を立てるところからスタートします。 $$\begin{eqnarray} ということになりますから、 $$\begin{eqnarray} という漸化式を得ます。 ここからは帰納法でもいいですが、帰納法を持ち出さずとも という数列 \(\{a_{k}^{2}-2b_{k}^{2}\}\) が常に定数である定数列であることを考えれば $$\begin{eqnarray} というように、手際よく処理できます。 なお、ペル方程式の基本的なシナリオや練習問題については 問題はこちら(画像をクリックするとPDFファイルで開きます。) 表向きは数学的帰納法の標準的な練習問題です。 本問を解くだけならば、そこまで難しい話ではありません。 (『数学的帰納法によ ... 続きを見る でシリーズものとして扱っています。 (3) よりペル方程式の自然数解をどんどん作り出すことができ、(2) よりそのペル方程式の自然数解から平方三角数がつくれることになります。 少し懸念すべきは、種となるペル方程式の自然数解 \((a_{k} \ , \ b_{k})\) の片割れ \(b_{k}\) が異なる値として無数に存在するかということです。 ただ、これに関しては $$\begin{eqnarray} という漸化式を得ていますし、数列 \(\{b_{n}\}\) が単調増加であるため、全て相異なる値をとることになります。 このことについてきちんと言及しておきましょう。(1) について
\(a\) が奇数であることについて
(2) について
(3) について
(3+2\sqrt{2})^{k+1} &=& (3+2\sqrt{2})(3+2\sqrt{2})^{k} \\
&=& (3+2\sqrt{2}) (a_{k}+b_{k}\sqrt{2})\\
&=& (3a_{k}+4b_{k})+(2a_{k}+3b_{k})\sqrt{2}
\end{eqnarray}$$
\left\{
\begin{array}{l}
a_{k+1} =3a_{k}+4b_{k} \\
b_{k+1} = 2a_{k}+3b_{k}
\end{array}
\right.
\end{eqnarray}$$
a_{k}^{2}-2b_{k}^{2}&=&a_{1}^{2}-2b_{1}^{2} \\
&=& 3^{2}-2 \cdot 2^{2}\\
&=& 1
\end{eqnarray}$$

参考ペル方程式 第1講 【ペル方程式とは】【ペル方程式の解とn乗展開】【2010年度 三重大学】
(4) について
\left\{
\begin{array}{l}
a_{k+1} =3a_{k}+4b_{k} \\
b_{k+1} = 2a_{k}+3b_{k}
\end{array}
\right.
\end{eqnarray}$$