問題はこちら(画像をクリックするとPDFファイルで開きます。)
いわゆるランダムウォーク(酔歩)と呼ばれる類の問題です。
様々なバリエーションがありますが、本問は正三角形上の辺を通って下段に降りていくという設定です。
この分野の問題らしく、その問題特有の設定や急所を見抜きながら対応していく「その場力」が必要な問題です。
計算量自体はそこまで多くはなく、洞察力寄りの力が求められます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む と丁寧に場合分けをして考えていきます。 という移動の仕方しかあり得ません。 この場合の確率は \(\displaystyle \frac{1}{2} \times \displaystyle \frac{1}{3}=\displaystyle \frac{1}{6}\) です。 と樹形図をかき、それぞれの場合を計算します。 ①が起こる確率は \(\displaystyle \frac{1}{2}\times\displaystyle \frac{1}{3}\times \displaystyle \frac{1}{2}=\displaystyle \frac{1}{12}\) ② が起こる確率は \(\displaystyle \frac{1}{2}\times\displaystyle \frac{1}{3}\times \displaystyle \frac{1}{3}=\displaystyle \frac{1}{18}\) ③ が起こる確率は \(\displaystyle \frac{1}{2}\times\displaystyle \frac{1}{3}\times \displaystyle \frac{1}{2}=\displaystyle \frac{1}{12}\) ですから、3回の移動で \(\mathrm{B}\) に到達する確率は \(\displaystyle \frac{1}{12}+\displaystyle \frac{1}{18}+\displaystyle \frac{1}{12}=\displaystyle \frac{2}{9}\) 以上から3回以下の移動で \(\mathrm{B}\) に到達する確率は \(\displaystyle \frac{1}{6}+\displaystyle \frac{2}{9}=\displaystyle \frac{7}{18}\) となります。 \(n\) 回「以下」の移動で \(\mathrm{B}\) に到達することは考えづらい事象です。 \( \ \ \ \ \ \ \ \vdots\) という場合を考えて全て加えるということを考えるのは少々骨が折れます。 そこで、直接考えるのが面倒であれば、余事象を考えるのがセオリーです。 ここで大切なのは、結局 \(n\) 回移動があった場合、起こり得る事象としては ということです。 したがって、「\(n\) 回以下の移動で \(\mathrm{B}\) にいる」ということの余事象は ということになります。 ここで、 とすると、対称性より \(b_{n}=c_{n}\) です。 したがって、先ほどの残りの という確率を \(p_{n}\) とすると \(b_{n}+c_{n}+p_{n}=1\) ですから、 \(2b_{n}+p_{n}=1\) すなわち \(b_{n}=\displaystyle \frac{1-p_{n}}{2}\) ということになります。 なので、この \(p_{n}\) が求まれば解決ということになるわけです。 という事象は、基本的に が移動の大半を占めており、複雑な移動ではありません。 余事象ではなく、直接考えてもできないことはありません。 ただ、その場合、 をきちんとする必要があります。 それに加えて ということはついてまわります。 これについては【戦略2】【解2】で触れてあります。(1) について
2回の移動でBに到達する場合
3回の移動でBに到達する場合
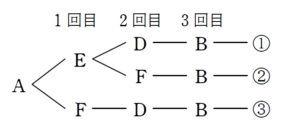
(2) について
余事象を正しく把握する
対称性の利用
直接考える方針について

