問題はこちら(画像をクリックするとPDFファイルで開きます。)
仮想難関大シリーズということで、東大、京大をはじめとする旧帝大、東工大、国公立大学医学部医学科などの難関国公立大を想定したオリジナルの自作問題です。
「手垢の付いていない問題で力試しがしたい」
という方はぜひご活用ください。
今回は座標に関する問題です。
円の極線という話題があります。
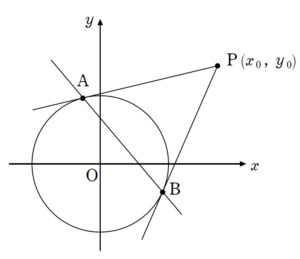
というように、円の外部の点から引いた2接線の2接点を通る直線を円の極線と言います。
本問はそれを放物線でやろうという問題です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む ひとまず状況を図示してみますと というような状況です。 接点を \(\mathrm{A}\)\((a \ , \ -a^{2})\) , \(\mathrm{B}\)\((b \ , \ -b^{2})\) と設定し、それぞれの接線の式を立式します。 \(y=-x^{2}\) に対して、\(y'=-2x\) ですから、 すなわち という2接線の式が得られ、これらが \((p \ , \ q)\) を通るため $$\begin{eqnarray} が得られます。 ここからは、円の極線という話題を経験しているかがモノを言う見方をします。 少し変形し $$\begin{eqnarray} とします。 これは ということを意味します。 もちろん2点\(\mathrm{A}\)\((a \ , \ -a^{2})\) , \(\mathrm{B}\)\((b \ , \ -b^{2})\)を通る直線は一つしかありませんから、直線 \(2px+y=-q\) が求める直線 \(\mathrm{AB}\) ということになります。 直線 \(\mathrm{AB}\) が手元にあるのであれば、 線分\(\mathrm{AB}\) を底辺と見て、点と直線の距離で高さを求める という作戦が自然でしょうか。 最終的に \(q=\displaystyle \frac{1}{p}\) という従属な2変数 \(p\) , \(q\) に関する最小値問題に帰着するということは見据えておきたいところです。 高さについては点 \((p \ , \ q)\) と直線 \(2px+y=-q\) との距離であり、\(p\) , \(q\) の式で与えられますが、底辺\(\mathrm{AB}\) の長さはいったん \(a\) , \(b\) の式で与えられます。 そこをどのように \(p\) , \(q\) の式に直すかということに注力していくことになります。 本家の円の極線を扱った入試問題は 問題はこちら(画像をクリックするとPDFファイルで開きます。) 極、極線という有名な構図があります。 その構図に関する有名事実をネタにした問題です。 工夫なしで立ち向かうとなると厳しい計算に襲われるか ... 続きを見る で扱っています。 どちらかというと、円の極線の導出は前提として、円の極線にまつわる性質的な部分にフォーカスを当てた問題であり、難問です。(1) について

\left\{
\begin{array}{l}
q = -2ap+a^{2} \\
q = -2bp+b^{2}
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
2pa-a^{2} = -q \\
2pb-b^{2} = -q
\end{array}
\right.
\end{eqnarray}$$
(2) について
円の極線について

参考極と極線【調和点列に関する話題】【1981年度 大分医科大学】

