問題はこちら(画像をクリックするとPDFファイルで開きます。)
この問題のオチは考えてみたくなります。
できることなら (1) や (2) の誘導なしで考えてみてほしいところですが、(1) , (2) 自体も筋が悪いとアタフタするかもしれません。
視覚的には
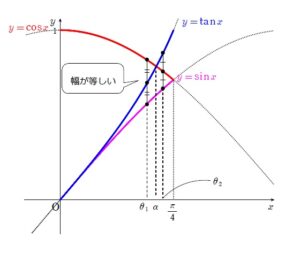
といった感じでグラフ的にとらえると、確かに題意の主張は納得できます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 基本的には微分してゴリゴリ路線です。 \(f'_{1}(x)\) を計算すると \(f'_{1}(x)=\displaystyle \frac{\sin^{3}{x}+\cos^{3}{x}-\sin{x}-2}{\cos^{2}{x}}\) と整理できます。 ここでいたずらに分子を \(g(x)\) とおいて \(\cdots\) などとしたら傷口が広がるだけです。 観察力の問題ですが、分子は \(0 \lt x \lt \alpha\) の範囲でざっくりと \((0.***\cdots)+(0.***\cdots)-(2.***\cdots)\) ですから負に決まっています。 ですから、\(f_{1}(x)\) は \(0 \lt x \lt \alpha\) の範囲で単調減少ということになります。 あとは \(f_{1}(0)\) と \(f_{1}(\alpha)\) の符号を調べ、それらが異符号であることを確認します。 これにより、「\(f_{1}(x)=0\) の解の存在 」が保証され、単調減少であることから「唯一性」も保証されます。 基本的には (1) と同様です。 \(f'_{2}(x)\) を計算すると \(f'_{2}(x)=\displaystyle \frac{1}{\cos^{2}{x}}+2\sin{x}-\cos{x}\) となります。 ここも観察力の問題で、 \(f'_{2}(x)=\displaystyle \frac{1-\cos^{3}{x}}{\cos^{2}{x}}+2\sin{x}\) と変形できますから、\(\alpha \lt x \lt \displaystyle \frac{\pi}{4}\) の範囲で \(f'_{2}(x) \gt 0\) であることが分かります。 ここから、\(f_{2}(x)\) は \(\alpha \lt x \lt \displaystyle \frac{\pi}{4}\) の範囲で単調増加ということになります。 もちろんこの後の作業は区間の始まりと終わりである \(f_{2}(\alpha)\) と \(f_{2}(\displaystyle \frac{\pi}{4})\) の符号が異符号であることを確認することです。 いよいよこの問題のオチです。 一般に 等差中項 \(a\) , \(b\) , \(c\) がこの順に等差数列となるとき \(\displaystyle \frac{a+c}{2}=b\) が成り立つ。 ということが言えます。 (1) の結果から \(\cos{x}-2\tan{x}+\sin{x}=0\) , すなわち \(\displaystyle \frac{\sin{x}+\cos{x}}{2}=\tan{x}\) を満たす \(x\) の存在が保証されています。 これにより、 という並びの等差数列の存在が保証されるわけです。 もちろん、(2) の結果も同様で \(\tan{x}-2\cos{x}+\sin{x}=0\) , すなわち \(\displaystyle \frac{\tan{x}+\sin{x}}{2}=\cos{x}\) を満たす \(x\) の存在が保証されていますので、 という並びの等差数列の存在が保証されるわけです。 そうなってくると、 真ん中が \(\sin{x}\) であるような並びである という並びが実現するかどうかに興味が行くわけです。 ただ、問題の主張的にこれは実現しないということが予想されます。 もちろん冒頭で描いたイメージ図からも真ん中が \(\sin{x}\) となることはないことが分かります。 (【解答】ではきちんと数式的に述べてあります。) (1) , (2) で示した内容は、出題者的には親切のつもりだとは思います。 ただ、範囲的に結構うるさいことになります。 数直線をイメージしてみましょう。 ということを(1) , (2) で証明したわけです。 問題では \(0 \lt \theta \lt \displaystyle \frac{\pi}{4}\) の範囲にちょうど 2 つ存在することを示せ。 ということが問われています。 そう考えると という疑問をつぶす必要が出てきます。 そういった意味で、出題側としては親切のつもりで出したのでしょうが、かえって話を鬱陶しくしています。 ただ、実際には \(0 \lt \theta \lt \displaystyle \frac{\pi}{4}\) 全体で \(f_{1}(x)=0\) , \(f_{2}(x)=0\) の実数解はそれぞれ 1 つしかない。 ということを確認するのはそれほど手間ではありません。 このあたりをどのタイミングで記述するかは悩ましいところですが、【解答】では (1) , (2) の証明の後に、この拡張した結果を記しておきました。 という実戦的な良問だと思います。(1) について
(2) について
(3) について
(1) の結果から
(2) の結果から
残る可能性
実は落とし穴が
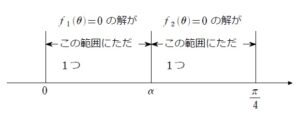
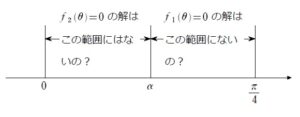
全体的に

