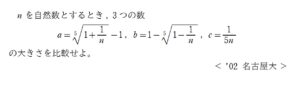問題はこちら(画像をクリックするとPDFファイルで開きます。)
今回のテーマ別演習では「一般化」という考え方を自分のモノにします。
問題文で与えられている特殊なシチュエーションを、より一般のシチュエーションに拡張して考えるという手法です。
このシリーズの一覧はコチラ
一般化 第1講【形から関数を設定する】【2015年度 信州大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 今回のテーマ別演習では「一般化」という考え方を自分のモノにします。 問題文で与えられている特殊なシチュエーションを、より一般のシチュエーションに拡張して考えるという手法です。 このシリーズの一覧はコチラ 第1講では、形から関数を設定する力を身につけることを目標とします。 例題の問題は非常にシンプルですが、しっかりと基礎的な部分で差が付きます。 数学の発想の素となる 「こういうことをしてみたい(調べてみたい)」 という素朴な気持ちや感性を鍛えて ...
一般化 第2講【欲しいものを準備する】【2002年度 名古屋大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 今回のテーマ別演習では「一般化」という考え方を自分のモノにします。 問題文で与えられている特殊なシチュエーションを、より一般のシチュエーションに拡張して考えるという手法です。 このシリーズの一覧はコチラ 第2講では、「欲しいものを準備する」ということをテーマとします。 基本的には第1講で学んだように、形を見て、 「これが欲しい」 という気持ちが湧きあがるかどうかが大切です。 今回は第1講の要素に加えて、少し深みのある問題です。 (以下ネタバレ ...
問題はこちら(画像をクリックするとPDFファイルで開きます。) 今回のテーマ別演習では「一般化」という考え方を自分のモノにします。 問題文で与えられている特殊なシチュエーションを、より一般のシチュエーションに拡張して考えるという手法です。 このシリーズの一覧はコチラ 第3講では、「定積分の扱い」ということをテーマとします。 今回のテーマである一般化以外にも様々な解法が考えられますが、今回のテーマに即した倒し方をぜひ考えてみてほしいと思います。 (以下ネタバレ注意) + クリック(タップ)して ...
例題はこちら(画像をクリックするとPDFファイルで開きます。) 類題はこちら(画像をクリックするとPDFファイルで開きます。) 類題2はこちら(画像をクリックするとPDFファイルで開きます。) 今回のテーマ別演習では「一般化」という考え方を自分のモノにします。 問題文で与えられている特殊なシチュエーションを、より一般のシチュエーションに拡張して考えるという手法です。 このシリーズの一覧はコチラ 第4講では、「分野の拡張」ということをテーマとします。 一般化することで強力な武器が手に入ることを実感してくださ ...
第2講では、「欲しいものを準備する」ということをテーマとします。
基本的には第1講で学んだように、形を見て、
「これが欲しい」
という気持ちが湧きあがるかどうかが大切です。
今回は第1講の要素に加えて、少し深みのある問題です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 今回比較する2数 \((1+\displaystyle \frac {2001}{2002})^{\frac{2002}{2001}}\) , \((1+\displaystyle \frac {2002}{2001})^{\frac{2001}{2002}}\) そのものを比べるというよりは、これらに自然対数をとった \(\displaystyle \frac {2002}{2001} \log{(1+\displaystyle \frac {2001}{2002})}\) , \(\displaystyle \frac {2001}{2002} \log{(1+\displaystyle \frac {2002}{2001})}\) を比較することを考えたいところです。 これを \(f(\displaystyle \frac {2002}{2001})\) と \(f(\displaystyle \frac {2001}{2002})\) の勝負 という形で見立てたいという気持ちから \(f(x)=x\log{(1+\displaystyle \frac {1}{x})}\) という関数の設定に辿り着くと思います。 微分すると \(f'(x)=\log{(1+\displaystyle \frac {1}{x})}-\displaystyle \frac {1}{x+1}\) という形が得られます。 そうなると次の興味は \(\log{(1+\displaystyle \frac {1}{x})}\) と \(\displaystyle \frac {1}{x+1}\) の大小 ということになりますから \(g(x)=\log{(1+\displaystyle \frac {1}{x})}-\displaystyle \frac {1}{x+1}\) と設定し、再び微分すると \(g'(x)=-\displaystyle \frac {1}{x(x+1)^{2}} \lt 0\) となり、\(x \gt 0\) の範囲で ということから , \(x \gt 0\) の範囲で \(g(x) \gt 0\) ということが言え、勝負ありです。 解答では、これを逆算的に(天下り的に)記述していきます。 実は実践演習 問題はこちら(画像をクリックするとPDFファイルで開きます。) 5乗根に関する数の大小比較の問題です。 目に付いた特徴によって様々な解法が考えられるあたりが面白いところです。 結論自体に辿り着くことは ... 続きを見る において、同じ 2002 年度の名古屋大学文系の問題を取り上げました。 この問題が、本問とどのように関わっているかについて【総括】の中で少し触れてあります。 ある意味、違う方面での「一般化」ということが言えるかもしれません。示すべき不等式をほぐす
次の興味
ちょっとした繋がり

参考累乗根と大小比較【2002年度 名古屋大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。)