例題はこちら(画像をクリックするとPDFファイルで開きます。)
類題はこちら(画像をクリックするとPDFファイルで開きます。)
フェルマー点と呼ばれる有名テーマについての問題を考えます。
例題では、フェルマー点の取り方と、なぜそう取ればよいのかについての証明を扱います。
類題は、フェルマー点を題材とした求値問題です。
特に断りがない限り、解答や戦略は「フェルマー点の知識を前提とせずに解くとしたら」という視点で解説してあります。
ひとまず以下はフェルマー点の概略について記しておきます。
フェルマー点とは
三角形 ABC に対して、3頂点 A , B , C への距離の和が最小となる点
を(三角形 ABC に対する)フェルマー点と言います。
120°以上の鈍角がある鈍角三角形だと、その鈍角を見込む頂点がフェルマー点となり、面白みはあまりありません。
そういった意味で以後、全ての内角が120°未満の三角形を対象として考えたいと思います。
フェルマー点の位置
結論だけ言ってしまうと
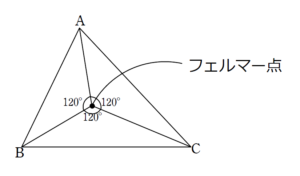
のように、
\(\angle{APB}=\angle{BPC}=\angle{CPA}=120^{\circ}\)
を満たす点 \(P\) がフェルマー点となります。
なぜかということを示すのが例題ということになります。
問題形式で考えることで自分のもとに手繰り寄せる感覚で自分のものにしてほしいと思います。


