例題はこちら（画像をクリックするとPDFファイルで開きます。）
不定方程式を解く際に、特殊解を見出して一般解に繋げる定番の話題ですが、連分数展開から特殊解に迫るという問題です。
特殊解を見出す手法として有名なのはユークリッドの互除法のプロセスに現れる
余りを余りで割り続ける
という手法ですが、今回の連分数展開と互除法のプロセスが手を繋いでいるという部分まで含めて見ていきます。
ユークリッドの互除法そのものについては
-
-
参考ユークリッドの互除法【原理の証明とイメージ】【2005年度 広島市立大学】
問題はこちら（画像をクリックするとPDFファイルで開きます。） ２つの正整数の最大公約数を求めるときに用いられる「ユークリッドの互除法」と呼ばれるアルゴリズムについて、原理と証明を考えてみます。 古典 ...
続きを見る
でしっかりと確認しておくとスムーズです。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む
連分数展開について
例えば \displaystyle \frac{8}{5} について考えてみます。
\displaystyle \frac{8}{5}=1+\displaystyle \frac {3}{5}
=1+\displaystyle \frac{1}{\displaystyle \frac{5}{3}}
=1+\displaystyle \frac{1}{1+\displaystyle \frac{2}{3}}
=1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{\displaystyle \frac{3}{2}}}
=1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{2}}}
というように、分数が連なっている形を連分数といい、連分数の形に変形していくことを連分数展開と言います。
特に、分子が 1 の形の連分数展開していくことを正則連分数展開と言います。
仮分数を帯分数に直すという意味
正則連分数展開は
\displaystyle \frac{8}{5}=1+\displaystyle \frac {3}{5}
というように仮分数を帯分数に直すという作業と
=1+\displaystyle \frac{1}{\displaystyle \frac{5}{3}}
というように逆数をとる作業の繰り返しです。
特に、帯分数に直した際の形は
商+\displaystyle \frac{余り}{分母}
であり、仮分数を帯分数に直す作業というのは
商と余りを出す作業
であることに他なりません。
分子にあった余りは逆数をとることによって、分母にやってきます。
つまり、逆数をとることで、余りで割るという作業になるということになります。
- 帯分数化によって余りを求める
- 逆数をとり（余りで割り）、再び帯分数化することで新たな商と余りを出す
という作業の繰り返しです。
互除法のプロセス
例えば \displaystyle \frac{18}{7} について互除法のプロセスを考えてみましょう。
（こんな簡単な数字に互除法を使うことなんかありませんが、連分数の作業と結びつけるためだと思ってください。）
- 18=7\cdot 2+4
- 7=4\cdot 1+3
- 4=3\cdot 1+1
- 3=1\cdot 3
これを連分数の作業と並べてみます。
- 18=7\cdot 2+4
\displaystyle \frac{18}{7}=2+\displaystyle \frac{4}{7}=2+\displaystyle \frac{1}{\displaystyle \frac{7}{4}}
- 7=4\cdot 1+3
2+\displaystyle \frac{1}{1+\displaystyle \frac{3}{4}}=2+\displaystyle \frac{1}{1+\displaystyle \frac{1}{\displaystyle \frac{4}{3}}}
- 4=3\cdot 1+1
2+\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{3}}}
- 3=1\cdot 3
連分数展開終了
というように対応するわけです。
１次不定方程式への応用について
a , b を互いに素な整数としたとき
ax+by=1
という形の整数解 (x \ , \ y) を考える際に
互除法のプロセスを用いて特殊解を見つける
というのがよく解説されている基本的な態度です。
ただ、上述したように、互除法のプロセスというのは正則連分数展開と対応します。
つまり、
連分数展開を利用して特殊解を見つけることもできるはずだ
ということでもあります。
それが例題の問題です。
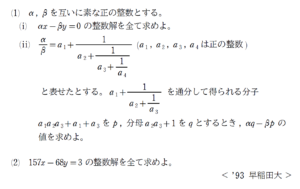
例題はこちら（再掲）（画像をクリックするとPDFファイルで開きます。）
最初にこの問題を見たときと、少し見え方が違ってきていると思います。
その見え方の違いが、問題を解く際にどう結び付くのかということを意識しながら取り組んでみてほしいと思います。
発展類題について
発展類題はこちら（画像をクリックするとPDFファイルで開きます。）
逆数を取って小数部分を考えるというのが今回の連分数展開と結びつくわけです。
(3) で示すべき内容は
有理数に対する正則連分数展開はどこかで終わる
ということです。
そして、\displaystyle \frac{p}{q} に対して
連分数展開が終わるまでの回数（互除法のプロセスにおける割り算の回数）は q 回以内に終わる
ということを意味しているわけです。
この結果は実はもう少し厳しく評価でき、それについては
こちらもCHECK
-
-
ラメの定理【ユークリッドの互除法の計算回数】
問題はこちら（画像をクリックするとPDFファイルで開きます。） ラメの定理と呼ばれる、ユークリッドの互除法のアルゴリズムの回数に関する上限を与える定理について考えてみます。 今回はラメの定理の主張を、 ...
続きを見る
で詳しく解説しています。
ただ、あまり変な先入観にとらわれて思考がぐらついてもいけないので、まずは手持ちの武器の中で戦ってみましょう。