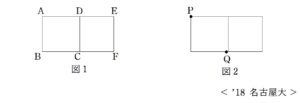
問題はこちら(画像をクリックするとPDFファイルで開きます。)
確率漸化式の標準問題の多くは、基本的な漸化式の処理力があれば、どちらかというと得点源になる分野です。
本問の場合、機械的な態度になりがちなこの分野の問題において、思考要素を含む問題であり、面白い良問だと思います。
確率の問題では
漸化式を導入するかどうか
ということは、方針決定において非常に大きな選択です。
通常の問題であれば、
「~~の確率を \(p_{n}\) とおく」
「\(p_{n+1}\) を \(p_{n}\) の式で表せ」
といった漸化式を匂わす設問が誘導としてありますが、難関大受験生としてはそれを期待してはいけません。
今回の問題も、見ただけでは漸化式の問題かどうかということは分からないでしょう。
実際のところ、漸化式を導入するかどうかについて、特効薬的なものがあるわけではないので、一括りにできない部分がありますが、
題意の事象が複雑であればあるほど、漸化式を設定したときには、それが逆に味方になることが多いです。
「同じことの繰り返し」、あるいは「限られた状態の中での推移」ということもシグナルの1つでしょう。
この辺りは場数を踏むことで、慣れていってもらうしかないと思います。
また、今回は本問をギブアップしてしまった人のために【リベンジ用問題】もつけておきましたので、ぜひリベンジしてもらえたらと思います。
【リベンジ問題】
(以下ネタバレ注意)