問題はこちら(画像をクリックするとPDFファイルで開きます。)
本問は教科書的な項目で言えば
陰関数の微分に関する力を見る問題
ということができるでしょう。
これから述べる背景的なものや、経験的な部分でアドバンテージをもてることはありますので是非今後の糧にしておきたい問題です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 接線の式を出すために まずは接線の式を出すために \(\displaystyle \frac{dy}{dx}\) を出す必要があります。 今回は \(y=f(x)\) の形ではなく、\(f(x \ , \ y)=0\) という形の関数 (陰関数) に対して\(\displaystyle \frac{dy}{dx}\) を出さなければいけません。 結論から言えば \(x^{\alpha}+y^{\alpha}=1\) の両辺を \(x\) で微分すると \(\alpha x^{\alpha-1}+\alpha y^{\alpha-1}\cdot\displaystyle \frac{dy}{dx}=0\) ということになり、ここから \(\displaystyle \frac{dy}{dx}=-(\displaystyle \frac{x}{y})^{\alpha-1}\) を得ます。 陰関数の微分の理解としては \(x^{\alpha}+y^{\alpha}=1\) 上の点 \((x \ , \ y)\) については \(x\) を決めたら \(y\) の値は決まる という構造をしており、気持ちの上で、\(y\) は \(x\) の値に応じて決まる値として、\(y=f(x)\) のように考えます。 このようにとらえ、\(x^{\alpha}+f(x)^{\alpha}=1\) の両辺を \(x\) で微分すると、合成関数の微分法から \(\alpha x^{\alpha-1}+\alpha f(x)^{\alpha-1}\cdot f'(x)=0\) ということになります。 これは \(\alpha x^{\alpha-1}+\alpha y^{\alpha-1}\cdot\displaystyle \frac{dy}{dx}=0\) という先ほどの式と同じことを意味していますね。 接線の式の導出後 とにもかくにも \(\displaystyle \frac{dy}{dx}\) が出せたのなら、接線の式が出せますから、\(x\) 切片、\(y\) 切片も導けることになります。 これにより、題意の線分 \(AB\) が式として導出できます。 もちろん、計算上は\(AB^{2}\) が一定値であるということを目指す方がよいでしょう。 この後の処理については【解答】を参照してください。 アステロイドについて アステロイドと呼ばれる曲線 ( \(x^{\frac{2}{3}}+y^{\frac{2}{3}}=1\) ) は本問のような、 接線が両座標軸によって切り取られる長さが一定である という性質をもっています。 これを経験している人からすると、\(\alpha=\displaystyle \frac{2}{3}\) というのはバレバレです。 しかし、それを前面に押し出すことは許されません。 アステロイドの概形としては のような形となります。 式としては アステロイドの式 陰関数表示:\(x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\) パラメーター表示:\(\begin{eqnarray} という式で与えられます。 アステロイドの登場の仕方 アステロイドは アステロイドの登場の仕方 と様々な切り口から問われる可能性があります。 このあたりは【総括】の中でも少し触れてありますので、ご確認ください。 関連付けて場数を踏みたい方へ 別の登場の仕方については 関連問題 問題はこちら(画像をクリックするとPDFファイルで開きます。) 【他の有名曲線を扱った問題はこちら】 さて、本問はサイクロイド3兄弟の一人、ハイポサイクロイドという有名曲線 ... 続きを見る も参考にしてください。 また、その他の有名曲線については 円の垂足曲線【動点の動く軌跡と動いた道のり】【2005年度 岡山大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 曲線上の動点 \(T\) における接線に、定点から下ろした垂線の足の軌跡を「垂足曲線」と言います。 本問は円の垂足曲線を扱った問題です。 (以下ネタバレ注意) + クリック(タップ)して続きを読む 一般的に垂足曲線は \(y=f(x)\) のような表示だと複雑になりますから、パラメータ表示(媒介変数表示)を用いて表現します。 ココがポイント ベクトルをつないでパラメータ表示 サイクロイド系の有名曲線もこのポイントの考え方でパラメ ... 有名曲線【エピサイクロイドと長さ】【1989年度 東京工業大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 【他の有名曲線を扱った問題はこちら】 さて、本問はサイクロイド3兄弟の一人、エピサイクロイドという有名曲線を扱った問題です。 サイクロイドとは ガムを踏んだタイヤが転がったときの、ガムの軌跡 です。 (以下ネタバレ注意) + クリック(タップ)して続きを読む どれだけ回転したかを表す量 \(\theta\) を導入すれば、点 \(P\) \((x \ , \ y)\) について $$\begin{eqnarray} ... 有名曲線【ハイポサイクロイド】【アステロイド】【2014年度 岐阜薬科大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 【他の有名曲線を扱った問題はこちら】 さて、本問はサイクロイド3兄弟の一人、ハイポサイクロイドという有名曲線を扱った問題です。 サイクロイドとは ガムを踏んだタイヤが転がったときの、ガムの軌跡 です。 (以下ネタバレ注意) + クリック(タップ)して続きを読む どれだけ回転したかを表す量 \(\theta\) を導入すれば、点 \(P\) \((x \ , \ y)\) について $$\begin{e ... 有名曲線【伸開線:インヴォリュート】【1998年度 武蔵工業大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 【他の有名曲線を扱った問題はこちら】 さて、本問は円の伸開線(インヴォリュート)と呼ばれる有名曲線を扱った問題です。 円に巻き付いた糸をたわむことなくほどいていったときの糸の先の軌跡です。 セロハンテープを伸ばすイメージに似ていますね。 本問では丁寧に図がついていますが、イメージして自分で図がかけると、立式のポイントを体で覚えられると思います。 (以下ネタバレ注意) + クリック(タップ)して続きを読 ... 有名曲線【カージオイド】【複素数平面からの問いかけ】【2005年度 早稲田大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 複素数平面の顔をしていますが、一皮むけば、有名曲線が現れます。 もちろん、その有名曲線特有の知識がなければ解けないとかはないのでご安心ください。 少しぼやくと 今回 \(|z|=1\) を動くとしか書いていません。 \(z\) が半径 1 の円をグルグル動けば、\(w\) も際限なく動き、点 \(w\) の描く曲線の長さは特定されません。 今回は非常に好意的に解釈し、 「重なっていない部分を曲線の長さとみなして」 考えました。 ... 有名曲線【アステロイド】【陰関数の微分】【1982年度 岐阜大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 本問は教科書的な項目で言えば 陰関数の微分に関する力を見る問題 ということができるでしょう。 これから述べる背景的なものや、経験的な部分でアドバンテージをもてることはありますので是非今後の糧にしておきたい問題です。 (以下ネタバレ注意) + クリック(タップ)して続きを読む 接線の式を出すために まずは接線の式を出すために \(\displaystyle \frac{dy}{dx}\) を出す必要があります。 今回は \(y=f ... 有名曲線【サイクロイド】【パラメーター表示された曲線の接線の扱い】【1988年度 岐阜大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) サイクロイドという有名曲線を扱った問題です。 サイクロイドとは ガムを踏んだタイヤが転がったときの、ガムの軌跡 です。 サイクロイドの中でも一番シンプルな地面を転がるタイプです。 パラメーター表示された曲線の扱いがしっかりしていれば、サイクロイドだということを知らなかったり、見抜けなかったとしても、問題自体は解くことができます。 ひとまずはパラメータ表示された曲線の扱いと言う部分の確認として利用してみてください。 本問は、簡単すぎず、難しすぎ ... 有名曲線【等角螺旋と特徴的な性質】【2000年度 神戸大学ほか】 例題はこちら(画像をクリックするとPDFファイルで開きます。) 有名曲線の一つである「等角螺旋」と呼ばれる曲線について扱った問題です。 対数螺旋、ベルヌーイの螺旋など様々な呼ばれ方がありますが、性質的なものと関連付けると等角螺旋という呼び方が「名が体を表す」ような呼び方なのでここではそう呼ばせてもらいます。 本問は教科書的な力で言えば 微分法の基本的な運用力 ベクトルを用いて座標平面上の角度を扱う力 パラメータ表示された曲線の弧長を求める力 が問われています。 上記の力をはかるためには、別に等角螺旋を題材 ... 有名曲線【カテナリー(懸垂線)】【2017年度 名古屋市立大学ほか】 例題はこちら(画像をクリックするとPDFファイルで開きます。) カテナリー(懸垂線)と呼ばれる有名曲線を扱った問題を見ていきます。 カテナリー(懸垂線)とは カテナリー(懸垂線)は鎖やロープの両端をもってぶら下げたときにできる曲線と紹介されるのが有名です。 カテナリー(懸垂線)を与える式 \(a\) は \(a \gt 0\) を満たす定数とするとき、カテナリー(懸垂線)を与える式は カテナリーを与える式 \(f(x)=\displaystyle \frac{a(e^{\frac{x}{a}}+e^{-\ ... 有名曲線【リサジュー曲線 (リサージュ 曲線)】【2014年度 同志社大学】 例題はこちら(画像をクリックするとPDFファイルで開きます。) リサジュー曲線と呼ばれる有名曲線について扱った問題です。 リサージュ曲線という呼ばれ方もあり、呼ばれ方に多少揺れがあります。 個人的にはリサージュの方が言いやすいですけど。 リサージュ曲線の定義 媒介変数 \(t\) を用いて リサージュ曲線 $$\begin{eqnarray} \left\{ \begin{array}{l} x = A \sin{at} \\ y = B \sin{(bt+\delta)} \end{array} \r ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) デカルトの正葉線という曲線についての問題です。 項目的には極座標で表された曲線が囲む面積ということになります。 (以下ネタバレ注意) + クリック(タップ)して続きを読む 極方程式について 与えられた \(x^{3}-3axy+y^{3}=0\) に \(x=r\cos{\theta}\) , \(y=r\sin{\theta}\) を代入すると \(r^{2}\{r(\cos^{3}{\theta}+\sin^{3}{\th ... 有名曲線【アルキメデスの螺旋(渦巻線)】【2002年度 京都大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) アルキメデスの螺旋(渦巻線)と呼ばれる有名曲線を扱った問題です。 アルキメデスの螺旋 \(a\) を \(a \gt 0\) なる定数としたとき、極方程式 \(r=a \theta\) で与えられる曲線をアルキメデスの螺旋(渦巻線)と言います。 本問はアルキメデスの螺旋の弧長について計算させる問題です。 結局差が付くのは最後の積分計算でしょう。 (以下ネタバレ注意) + クリック(タップ)して続きを読む (1) について 良くも ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) レムニスケート(連珠形)と呼ばれる有名曲線を題材とし、 直交座標表示と極方程式との結びつき 極方程式で表される曲線の面積 について学習します。 正直極方程式はウルサイ議論が多く、記述で抜かりなくまとめるには神経を使うので疲れる分野に感じる人も多いでしょう。 そのあたりについては「方程式」という言葉の意味を噛み砕いていけば、押さえるべき部分というのがある程度は見えると思います。 どうやって解答をまとめようかという「記述のまとめ方」みたいなところ ... 2022年度 九州大学 理系第5問【パラメータ表示された曲線】【ハイポサイクロイドの概形と面積】 問題はこちら(画像をクリックするとPDFファイルで開きます。) パラメータ表示された曲線に関する概形と面積について考える定番の話題です。 最終的にこの曲線 \(C\) の概形を図示することになりますが、それに向けてうまく工夫して考えるように誘導がついています。 誘導に乗れるかどうかということは、誘導のありがたみを感じることができるかどうかということです。 \(x\) 軸についての対称性 \(\displaystyle \frac{\pi}{3}\) ごとの回転対称性 という「対称性」を駆使し、省エネしなが ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) ルーローの三角形と呼ばれる有名図形を扱った問題です。 出典は1987年度の某全国模試です。 本問のオチは原点にあるルーローの三角形の一頂点の軌跡を捉え、その曲線の長さを求めるという問題です。 頭の中でどのような動きをするのかを追っていく必要があり、動的処理から逃げることはできません。 ロータリーエンジンの原理にも使われていたり、パナソニックのルーロという掃除機もこのルーローの三角形が元となっているなど、実用的にも色々応用されています。 (以下 ... 有名曲線【トロコイド】【2012年度 お茶の水女子大学ほか】 例題はこちら(画像をクリックするとPDFファイルで開きます。) 類題はこちら(画像をクリックするとPDFファイルで開きます。) トロコイドという有名曲線を扱った問題です。 トロコイドとは 円が滑らずに転がったときの円の内部または外部の定点の軌跡 です。 円周上の定点の軌跡はサイクロイドと呼ばれる有名曲線です。 基本的にはサイクロイドに準ずる態度でトロコイドのパラメータ表示を得ていきます。 ひとまずサイクロイドに関してまだ足元がグラグラということであれば でサイクロイドについての問題を扱っています。 (以下 ... アステロイドの射影【ベクトル方程式の活用】【1999年度 お茶の水女子大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) アステロイドに光を当てたときにできる影について考える問題です。 立式さえできれば、曲線の長さという基本的な計算になりますので、この影が表す図形をどのように立式するかがポイントになってきます。 (以下ネタバレ注意) + クリック(タップ)して続きを読む イメージ図 ひとまずは問題の図形 \(D\) , \(D'\) のイメージを掴みたいと思います。 図形 \(D\) の境界線が表す曲線を \(C\) , 図形 \(D'\) の境界線が表す曲 ... も適宜どうぞ。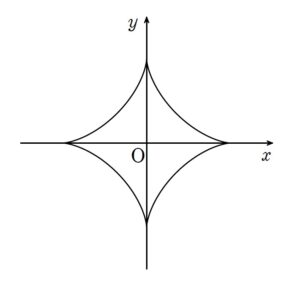
\left\{
\begin{array}{l}
x = a\cos^{3}{t} \\
y = a\sin^{3}{t}
\end{array}
\right.
\end{eqnarray}\)

有名曲線【ハイポサイクロイド】【アステロイド】【2014年度 岐阜薬科大学】
【他の有名曲線を扱った問題はこちら】


















