例題はこちら(画像をクリックするとPDFファイルで開きます。)
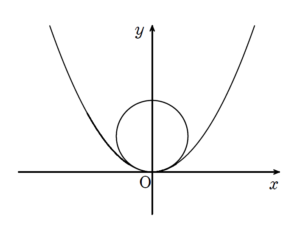
放物線に接する外接円の列に関する座標と数列の融合問題です。
- 放物線と円が接するという状態をどのように捌いていくか
- それによって得られた数列をいかに捌いていくか
という部分が山場となります。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む ひとまず今回の円 \(O_{n}\) の方程式を立式するために、中心の座標と半径を設定することにします。 中心を \((0 \ , \ a_{n})\) , 半径を \(r_{n}\) とすると、円 \(O_{n}\) の方程式は \(x^{2}+(y-a_{n})^{2}={r_{n}}^{2}\) ということになります。 これと放物線 \(y=x^{2}\) が2点で接するということをどのように捌いていくかが最初のポイントです。 次数が低い方がよいと考えれば、\(y=x^{2}\) と \(x^{2}+(y-a_{n})^{2}={r_{n}}^{2}\) を連立して \(x^{2}\) を消去すると \(y+(y-a_{n})^{2}={r_{n}}^{2}\) ということになり、これを整理すると \(y^{2}-(2a_{n}-1)y+{a_{n}}^{2}-{r_{n}}^{2}=0\) という \(y\) の2次方程式を得ます。 これが正の重解をもてばよく、ひとまず判別式 \(D\) について \(D=0\) を処理していきます。 これにより、 \(a_{n}={r_{n}}^{2}+\displaystyle \frac{1}{4}\) という関係式を得ます。 \(y=x^{2}\) と \(x^{2}+(y-a_{n})^{2}={r_{n}}^{2}\) を連立して \(y\) を消去すると \(x^{2}+(x^{2}-a_{n})^{2}={r_{n}}^{2}\) ということになり、これを整理すると \(x^{4}-(2a_{n}-1)x^{2}+{a_{n}}^{2}-{r_{n}}^{2}=0\) と、\(x\) の4次方程式を得ます。 一般に、これが4つの実数解をもつとすると、対称性から \(x=\alpha \ , \ \beta \ , \ -\alpha \ , \ -\beta\) という形となります。 これにより、 \(x^{4}-(2a_{n}-1)x^{2}+{a_{n}}^{2}-{r_{n}}^{2}=(x-\alpha)(x+\alpha)(x-\beta)(x+\beta)\) すなわち \(x^{4}-(2a_{n}-1)x^{2}+{a_{n}}^{2}-{r_{n}}^{2}=(x^{2}-{\alpha}^{2})(x^{2}-{\beta}^{2})\) という形に因数分解できることになります。 特に今回の というシチュエーションは \(\alpha=\beta\) のときを考えればよく \(x^{4}-(2a_{n}-1)x^{2}+{a_{n}}^{2}-{r_{n}}^{2}=(x^{2}-{\alpha}^{2})^{2}\) すなわち \(x^{4}-(2a_{n}-1)x^{2}+{a_{n}}^{2}-{r_{n}}^{2}=x^{4}-2{\alpha}^{2}x^{2}+{\alpha}^{4}\) が \(x\) についての恒等式ということになり、係数を比較すればよいでしょう。 この路線で捌いても、 \(a_{n}={r_{n}}^{2}+\displaystyle \frac{1}{4}\) を得ることになります。 2円 \(O_{n}\) , \(O_{n-1}\) 外接するという条件から \(a_{n}-a_{n-1}=r_{n}+r_{n-1}\) という関係式も得ることができます。 先ほどの \(a_{n}={r_{n}}^{2}+\displaystyle \frac{1}{4}\) という関係式と合わせて考えていきます。 方針としては一文字消去ということで、消しやすい \(a_{n}\) を消していけばよいでしょう。 この連立漸化式を捌き、\(a_{n}\) , \(r_{n}\) を出せれば、中心の座標と半径が分かるため、本問は解決です。 例題の確認問題です。 (1) については (2) を片付ければ同時に片付きます。 放物線と円が接するという状況としては、例題や類題1のように というように2点で接するという状況もあれば という状況もあります。 本問はこの接し方についても扱います。 なお、円と放物線の共有点の個数については 例題はこちら(画像をクリックするとPDFファイルで開きます。) 放物線と円の共有点の個数について直球で訊いている問題です。 放物線と円の共有点については結構ウルサイので、場当たり的になってしまうことも ... 続きを見る で本腰を入れて解説しています。設定
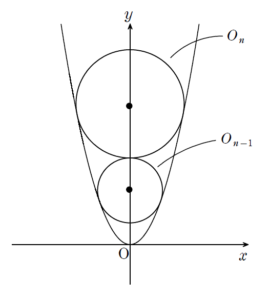
路線1:\(x^{2}\) を消去する
路線2:\(y\) を消去する
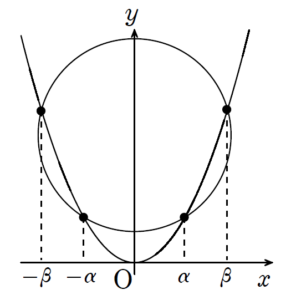
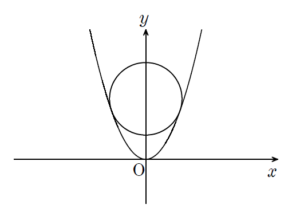
外接条件
類題1について
類題1はこちら(画像をクリックするとPDFファイルで開きます。)
類題2について
類題2はこちら(画像をクリックするとPDFファイルで開きます。)
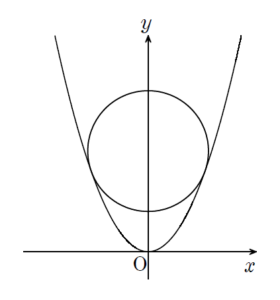

参考放物線と円の共有点の個数【方程式の解の意味】【2015年度 大阪市立大学ほか】



