問題はこちら(画像をクリックするとPDFファイルで開きます。)
まずは問題の舞台設定を把握するところからエネルギーを使います。
ベクトルで表現されていますがこの \(V_{a}\) , \(V_{b}\) というのは言ってみれば
斜めに傾いた円柱
です。
この斜めに傾いた円柱同士の共通部分の体積を求めるのが本問の趣旨となります。
目を凝らしても見づらいですから、何とかして工夫することを考えましょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 今回の立体は \(\overrightarrow{ OR }=\overrightarrow{ OP }+\overrightarrow{ OQ }\) というベクトル方程式で表された立体です。 \(P\) が 線分\(OA\) 上を動きます。 その後、その点 \(P\) を中心として、回転ベクトル \(\overrightarrow{ OQ }\) を繋ぐわけですから、イメージとしては以下の図のようになります。 \(V_{b}\) についても同様です。 とりあえず今は見やすさ優先で離して描きましたが、本来は点 \(O\) を共有するようにガッチャンコしているわけです。 こういった見づらい立体への対応の有力候補は という方針です。 連立不等式という式で表現してしまうことにより、体積を求めるために必要な断面、及び断面積を式に教えてもらおうという魂胆の作戦です。 しかし、今回はこの「斜めに傾いた円柱」を直交座標 \(x\) , \(y\) , \(z\) の式として表現するのが困難です。 したがって、連立不等式で表そうにも \(x\) , \(y\) , \(z\) に関する不等式を得るのが難しそうです。 なので、この方針に拘るとかえって身動きがとれなくなりかねません。 潔く次の一手を考えます。 見づらい立体への対応策として、もう一つ有力な考え方が 「切ってからガッチャンコ」 という態度です。 先にガッチャンコしてしまうから訳が分からなくなります。 そこで、まず切ります。 気持ちとしてはとにかく断面積を把握できればそれでいいわけです。 斜めっていようが \(z=k\) というように、\(z\) 軸に垂直に切れば、切り口は円です。 \(V_{a}\) の断面も \(V_{b}\) の断面もともに円です。 この状態からガッチャンコすれば、題意の立体(全体像は謎)を\(z=k\) で切った断面は 円の内部と円の内部の共通部分 と途端にイメージできるようになります。 人間の目と言うのは不思議なものですね。順番を変えただけで途端に見える景色が変わってしまいます。 順番を変えたからといって不都合は生じません。 はどちらも同じものです。 今回は \(z=\cos{\theta}\) で切れという指示があります。 これについては個人的には余計なお世話です。 普通に \(z=k\) で切ったときの断面に円が現れた時点で、角度 \(\theta\) は言われなくても自分で導入します。 下手に \(z=\cos{\theta}\) で切れと言われると どこが \(\theta\) だ? と探す羽目になり、かえって鬱陶しいです。 (1) で得た断面積 \(S\) は \(\theta\) の式として得られます。 だからと言って \(\displaystyle \int_{ \ }^{ \ }S d\theta\) としてはものの見事に間違いです。 \(z=○\) で切ったのであれば、途中どんな文字が現れようとも、\(\displaystyle \int_{ \ }^{ \ }S dz\) です。 あなたが最後に書く式は切った時点で決まっている ということを忘れないでください。 例題はこちら(画像をクリックするとPDFファイルで開きます。) 「不等式で表された立体の体積」というテーマ性のある問題を扱います。 このあたりを場当たり的に何となく理解している状況から、自分が何をして ... 続きを見る 問題はこちら(画像をクリックするとPDFファイルで開きます。) 円柱と円錐の共通部分の体積についての問題です。 東大は昔から立体図形を扱った体積に関する出題が目立ちます。 東大に限らず、 ... 続きを見る 例題はこちら(画像をクリックするとPDFファイルで開きます。) 初見だと何から手を付ければよいか戸惑う人も多いと思います。 以前に 併せてどうぞ 不等式で表された立体という内容を扱いました。 今回はそ ... 続きを見る も必要に応じてご活用ください。今回の立体のイメージ
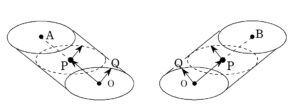
見づらい立体への対応の有力候補
次の一手としては
今回の問い方は余計なお世話?
(2) について
見づらい立体への対応シリーズ
連立不等式で表された立体への対応(基礎)

不等式で表された立体の体積【2007年度 北海道大学】
見づらい立体を不等式で表す(応用)

円柱と円錐の共通部分の体積【見づらい立体への対応】【2003年度 東京大学】

円柱と円柱の共通部分の体積【見づらい立体への対応】【有名問題】

