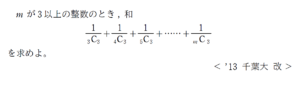問題はこちら(画像をクリックするとPDFファイルで開きます。)
二項係数の逆数の和を求める問題です。
シグマ計算の基本については以前
テーマ別演習:シグマ計算基本方針
シグマ計算基本方針 第1講【公式確認とその延長】【2010年度 九州大学など】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 今回からテーマ別演習でパターン性の濃い計算技法を扱っていこうと思います。 今回のテーマは「シグマ計算」です。 このシリーズの一覧はこちら 最初にまとめておきます。 シグマ計算の基本方針は次の3つです。 シグマ計算基本方針 公式利用とその延長 差分解からの和の中抜け 二項定理の活用 第1講はまずシグマ計算の公式の確認と、その延長について扱います。 手始めにまずは上の問題で公式の確認と、その証明をしてみてください。 最 ...
シグマ計算基本方針 第2講【差分解からの和の中抜け】【2013年度 兵庫県立大学など】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 【有理化】 【部分分数分解】 テーマ別演習「シグマ計算基本方針」第2講です。 このシリーズの一覧はこちら シグマ計算の基本方針は次の3つです。 シグマ計算基本方針 公式利用とその延長 差分解からの和の中抜け 二項定理の活用 今回の第2講では 差分解からの和の中抜け を扱います。 差分解からの和の中抜けとは \(\displaystyle \sum_{k=1}^n (b_{k}-b_{k+1})\) とシグマの中身を差の形に見ることで \((b ...
シグマ計算基本方針 第3講【二項定理の活用】【2007年度 大阪府立大学ほか】
問題はこちら(画像をクリックするとPDFファイルで開きます。) テーマ別演習「シグマ計算基本方針」第3講です。 このシリーズの一覧はこちら シグマ計算の基本方針は次の3つです。 シグマ計算基本方針 公式利用とその延長 差分解からの和の中抜け 二項定理の活用 今回の第3講では 二項定理の活用 を扱います。 二項定理を活用してシグマ計算する場面は特徴的であり、 二項定理を使うシグマ計算 コンビネーションのシグマ というのが見落としてはならない特徴であり、キーワードです。 ただ、単純に代入すればいいだけでなく、 ...
シグマ計算基本方針 第4講【応用実践】【2005年度 大分大学ほか】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 【1】(以下ネタバレ注意) + クリック(タップ)して続きを読む 連続自然数の積のシグマ計算は工夫の余地があります。 バラバラに展開してしまった人は「ジェイソン」と呼ばせていただきます。 バラバラにして\(\displaystyle \sum_{k=1}^n k\) , \(\displaystyle \sum_{k=1}^n k^{2}\) , \(\cdots\) などを使って計算していくのは流石にシンドイと思います。 和の中抜けを ...
シグマ計算基本方針 第5講【二項係数の2乗和】【経験値が必要】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 初見かつノーヒントであれば厳しいと思います。 まずはノーヒントで粘れるだけ粘ってみてください。 どうにも埒があかないな、となったら誘導付きの問題も用意しましたので、そちらで再チャレンジしてみてください。 + クリック(タップ)して誘導付きの問題でチャレンジする 誘導付きはこちら(画像をクリックするとPDFファイルで開きます。) \((1+x)^{2n}\) という式を考えるという部分が見えるだけでも、気持ち的には楽でしょう。 と ...
シグマ計算基本方針 第6講【二項係数の交代和】【2005年度 山形大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 今回扱うのは二項係数の符号が入れ違いになっている和(交代和)について考えます。 前半部分は第3講で扱った「二項定理の活用」という話題です。 「\((1+x)^{n}\) の展開式を用いて」というのはここまで勉強してきた人からすると正直余計なお世話でしょう。 (ii) の偶数番目だけを取り出したい、奇数番目だけを取り出したい、という問題についても (i) で考えた \(a\) , \(b\) を利用 ...
シグマ計算基本方針 第7講【3つ飛ばしの二項係数の和】【1997年度 岐阜大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) このシリーズの一覧はこちら 今回扱うのは3つ飛ばしの二項係数の和について扱います。 原題ではもう少し段階的な設問がありましたが、言われたことをやっているうちに終わってしまい、作業感が強かったため、考えてもらいたい部分については一部カットしました。 (以下ネタバレ注意) + クリック(タップ)して続きを読む (1) について 二項定理の活用により仕留める方針が第一感です。 \((1+x)^{n}={}_{n} \ma ...
というシリーズで扱っています。
今回は、基本がしっかり身についているということは前提で、手持ちの武器の中で何をどう選び活用していくかという運用力を試すという目的で実践演習で扱います。
なお、原題は誘導がありましたが、方針も含めて考えるという意味で誘導は外しました。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 今回求める和は \(\displaystyle \sum_{k=3}^{m}\displaystyle \frac{1}{{}_k \mathrm{ C }_3}\) です。 \(\displaystyle \frac{1}{{}_k \mathrm{ C }_3}=\displaystyle \frac{6}{k(k-1)(k-2)}\) ですから、 \(\displaystyle \sum_{k=3}^{m}\displaystyle \frac{1}{{}_k \mathrm{ C }_3}=\displaystyle \sum_{k=3}^{m}\displaystyle \frac{6}{k(k-1)(k-2)}\) を求めればよいことになります。 ここまでくれば、\(\displaystyle \frac{6}{k(k-1)(k-2)}\) を部分分数分解によって差分解し、和の中抜けを狙っていく目途が立ちます。 振り返ってみると、本問は二項係数の顔をしていますが、実際には分数形のシグマとしての問題であったと言えましょう。