例題はこちら(画像をクリックするとPDFファイルで開きます。)
「不等式で表された立体の体積」というテーマ性のある問題を扱います。
このあたりを場当たり的に何となく理解している状況から、自分が何をしているのかはっきりと説明できる状態に昇華させるためには
方程式や不等式というものの根っこ
をおさえる必要があります。
ここではそこをガッチリと掴みながらこのトピックスはもちろん、その他の問題に対しても役に立つ考え方を身につけていってほしいと思います。
(以下ネタバレ注意)
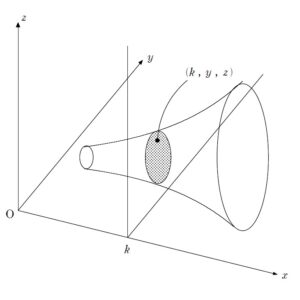
+ クリック(タップ)して続きを読む 方程式 \(y=2x+1\) が表す図形は「直線」とすぐ答えられると思います。 もう少し厳密に言うと 「この \(=\) を満たす点 \((x \ , \ y)\) 集まれ~」 と呼びかけて集まってきた点 \((x \ , \ y)\) の集合体が直線ということです。 不等式が表す立体も同じです。 「この不等号を満たす点 \((x \ , \ y \ , \ z)\) 集まれ~」 と呼びかけて集まってきた点 \((x \ , \ y \ , \ z)\) の集合体が、その不等式が表す図形です。 仮に集まってきた集合体が次のような立体だったとしましょう。 その立体を例えば平面 \(x=k\) で切った切り口は \((k \ , \ y \ , \ z)\) の集合 ですね。 不等式を満たす点 \((x \ , \ y \ , \ z)\) たちの中で \(x\) 座標が \(k\) となるような連中 が平面 \(x=k\) で切った切り口になるのです。 基本的にどんな立体か想像できないと思います。 ただ、心配しなくても大丈夫です。 目をつぶって切ってください。 断面は式が教えてくれます。 不等式で表された立体の体積のポイント この中でも3つめの \(x=k\) , \(y=k\) , \(z=k\) のどれで切るかの判断ですが、基本的には次のような観点から切る文字を選びます。 切る文字の選択基準 判断基準1:次数の高い文字 判断基準2:登場回数が多い文字 判断基準3:対称性がある場合は対称性を考慮 今回の例題では \(z=k\) で切ります。 するとその後、その \(z\) は \(k\) となって「定数扱い」になります。 定数になってくれるわけですから、 次数が高く、そのままだと厄介であったり、至る所に登場して出しゃばっている文字に定数となって消えていただく のが計算を進めるにあたり得策であるからです。 今回は \(x\) , \(y\) について対称性があるため、対称性の外にいる \(z\) に注目し、\(z=k\) で切ります。 もちろん、上述の判断基準には例外もあります。 ただ一つ言えることとして、上の判断基準の目的は 「その後の図示が楽になるようにする」 ということです。 手段だけを覚えて目的を理解しないと応用が利かないので、目的をしっかりと理解しておきましょう。 例題で学んだことが自分のものになっているかの確認にご利用ください。 問題はこちら(画像をクリックするとPDFファイルで開きます。) 円柱と円錐の共通部分の体積についての問題です。 東大は昔から立体図形を扱った体積に関する出題が目立ちます。 東大に限らず、 ... 例題はこちら(画像をクリックするとPDFファイルで開きます。) 初見だと何から手を付ければよいか戸惑う人も多いと思います。 以前に 併せてどうぞ 不等式で表された立体という内容を扱いました。 今回はそ ... 方程式・不等式が表す図形とは
例えば
不等式も同じ
例題について
不等式で表された立体の体積についての処方箋
注意
復習用問題について
復習用問題はこちら(画像をクリックするとPDFファイルで開きます。)
関連実践問題

円柱と円錐の共通部分の体積【見づらい立体への対応】【2003年度 東京大学】

円柱と円柱の共通部分の体積【見づらい立体への対応】【有名問題】


