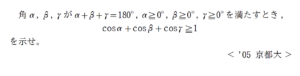問題はこちら(画像をクリックするとPDFファイルで開きます。)
三角形の内角に関する不等式で、シンプルな題意です。
解法も様々考えられ、京大らしい問題だと思います。
試験場では愚直に解くのが現実的ですが、時間無制限で頭を鍛えるという点においては別解を考えるいい題材となるでしょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 目標 \(\cos{\alpha}+\cos{\beta}+\cos{\gamma}-1 \geq 0\) が目標であることは睨んでおきます。 従属な3変数なので、ひとまずは 文字消去 を狙っていきます。 ここでは \(\gamma=180^{\circ}-(\alpha+\beta)\) と、\(\gamma\) を消そうと思います。 すると、 \(\cos{\alpha}+\cos{\beta}+\cos{\gamma}-1=\cos{\alpha}+\cos{\beta}+\cos{\{180^{\circ}-(\alpha+\beta)\}}-1\) \(=\cos{\alpha}+\cos{\beta}-\cos{(\alpha+\beta)}-1\) となります。 ここからは、不等式証明と相性のよい積の形を狙って 和積公式 を用いて話を進めていくことを目論んでいきます。 ここから先も各種三角関数の式変形に関する運用力が問われます。 この路線は【解1】で扱っています。 与えられた角度は 三角形の内角 を彷彿とさせる角度です。 ただ、\(0^{\circ}\) や \(180^{\circ}\) なども許される設定です。 こういったウルサイ細々としたものは個別にチャッチャと検証して片づけます。 対称性から \(0^{\circ} \leq \gamma \leq \beta \leq \alpha \leq 180^{\circ}\) として考えても一般性を失いません。 上記の細かいことを抜きにして \(\alpha\) , \(\beta\) , \(\gamma\) が三角形の内角としての角度だとします。 すると、最大角は \(\alpha\) ということですから、 \(\beta\) , \(\gamma\) は鋭角 ということが言えます。 ここで 第1余弦定理 ということが言えます。 特に、今回は の辺々を加えると \(b+c=(b+c)\cos{\alpha}+a(\cos{\beta}+\cos{\gamma})\) ということが言え、 \((b+c)(1-\cos{\alpha})=a(\cos{\beta}+\cos{\gamma})\) すなわちa \(1-\cos{\alpha}=\displaystyle \frac{a}{b+c}(\cos{\beta}+\cos{\gamma})\) を得ます。 三角形の成立条件から \(a \leq b+c\) なので、 \(\displaystyle \frac{a}{b+c} \leq 1\) です。 角度の大小を設定しておいたおかげで、\(\beta\) , \(\gamma\) は鋭角です。 なので、\(\cos{\beta} \gt 0\) , \(\cos{\gamma} \gt 0\) ということになりますから \(\displaystyle \frac{a}{b+c}(\cos{\beta}+\cos{\gamma}) \leq \cos{\beta}+\cos{\gamma}\) であるため、 \(1-\cos{\alpha} \leq \cos{\beta}+\cos{\gamma}\) すなわち \(\cos{\alpha}+\cos{\beta}+\cos{\gamma} \geq 1\) という示すべき不等式が得られます。 例えば \(\vec{a}\) , \(\vec{b}\) のなす角度を \(\alpha\) としたとき \(\cos{\alpha}=\displaystyle \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\) です。 できる限りシンプルに設定したいので、 \(|\vec{a}|=1\) , \(|\vec{b}|=1\) というように設定すれば \(\cos{\alpha}=\vec{a} \cdot \vec{b}\) と、コサインが内積で表現できます。 そこで という図のように \(\alpha\) , \(\beta\) , \(\gamma\) を設定してやります。 この路線は【解3】で扱っています。 第1余弦定理を用いる方針2や、ベクトルの内積とみる方針3はどちらかと言えば観賞用の解答に近いでしょう。 試験場では和積公式を用いてゴリゴリほぐしていくのが現実的だと思います。 楽しむのは試験が終わってからでいいので、試験場では泥臭くても確保することを優先的に考えていきましょう。 精力的に学習を進めていくと、なまじ色々見えるため 「何かあるのか」 と疑ってしまいがちですが、そこに引きずり込まれると深みに嵌まります。 策士策に溺れるということがないように気をつけてくださいね。 問題はこちら(画像をクリックするとPDFファイルで開きます。) 非常にシンプルな問題です。 切れ味鋭く捌くこともできますし、腕力で押し切ることもできます。 いずれの路線にせよ、確かな力が必要です。 類 ... 続きを見る 問題はこちら(画像をクリックするとPDFファイルで開きます。) シンプルな問題ですが、多くの解法が考えられ、それぞれ色々な教訓を含んでいるので、一粒で何度もおいしい問題です。 どういう視点からこの問題 ... 続きを見る 類題も適宜活用してください。方針1:和積公式
方針2:第1余弦定理の活用
対称性を利用して大小関係を導入
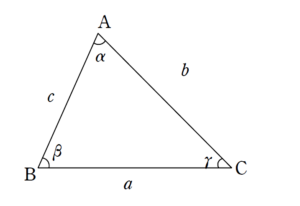
方針3:ベクトルの内積の利用
まとめ
類題

参考三角形の内角のtanの和【1966年度 金沢大学】

参考三角関数の積の最大値【従属3変数】【1999年度 京都大学】