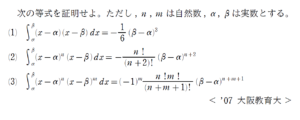ベータ関数【６分の１公式などの拡張】【2015年度横浜市立大学ほか】

例題はこちら（画像をクリックするとPDFファイルで開きます。）

通称 $\displaystyle \frac{1}{6}$ 公式や $\displaystyle \frac{1}{12}$ 公式と呼ばれる積分公式の一般化であるオイラーの第一種積分、ベータ関数がバックボーンにある問題を扱います。

これらの名前は入試的には無理に覚えなくてもいいですが、シナリオについては難関大受験生としては一度は経験しておきたいです。

入試段階では「こんな話題だな」という頭のラベル付けとして覚えるぐらいの感覚で十分です。

本格的に学ぶのは大学入学以降になります。

フライングしてもっと深く突っ込んで解説してくれよという意欲満々の人には申し訳ないですが、あくまで大学受験の話題としての位置づけを逸脱しない程度の解説にとどめておきたいと思います。

（以下ネタバレ注意）

+ クリック（タップ）して続きを読む

例題について

(1) について

$B(3 \ , \ 2)=\displaystyle \int_{0}^{1}x^{3}(1-x)^{2} dx$

という具体的な積分計算です。

煮るなり焼くなりしてほしいですが、最悪調理の工夫をせず生で齧るという選択肢すらあります。

ここでは後の方針と一貫性をもたせるために、部分積分で調理します。

部分積分

$\displaystyle \int_{ \ }^{ \ } f'(x)g(x) dx=f(x)g(x)-\displaystyle \int_{ \ }^{ \ }f(x)g'(x) dx$

の旨味を引き出す見方は

ダッシュの服の着せ替え

という見方です。

最終的に鬱陶しいのは $(1-x)^{2}$ という部分ですからこいつにダッシュの服を着せかえて次数を下げていくという使い方をします。

(2) について

漸化式的なものを作れという指示です。

積分が絡む漸化式については部分積分で作るのが常套手段です。

今回は

「 $n$ の方の次数を下げよ」

という指示ですから、

$\displaystyle \int_{0}^{1}x^{m}(1-x)^{n} dx=\displaystyle \int_{0}^{1} (\displaystyle \frac{1}{m+1}x^{m+1})'(1-x)^{n} dx$

と見て部分積分をかましていけばよいでしょう。

(3) について

(2) が正しく計算できていれば

$B(m \ , \ n)=\displaystyle \frac{n}{m+1}B(m+1 \ , \ n-1)$

という結果が得られていると思います。

この漸化式を順次用いていくと、やがて

$B(☆ \ , \ 0)$

というように、 $(1-x)$ 側の次数が 0 となり、消える瞬間が訪れます。

(4) について

今回の $B(m \ , \ n)$ を登場させたいので、 $B(m \ , \ n)$ を登場させるような置換積分を考えていきます。

まず、被積分関数 ( インテグラルの中身 ) の形を整えたいので

$x-a=t$

などと置換します。

積分区間や積分変数の変数変換に注意すると

$\displaystyle \int_{a}^{b}(x-a)^{m}(x-b)^{n}dx=\displaystyle \int_{0}^{b-a}t^{m}\{t-(b-a)\}^{n} dt$

となります。

積分区間を $[0 \ , \ 1]$ としたいので、

$t=(b-a)s$

と置換します。

これにより

$\displaystyle \int_{0}^{b-a} t^{m}\{t-(b-a)\}^{n} dt=\displaystyle \int_{0}^{1} (b-a)^{m}s^{m}\{(b-a)s-(b-a)\}^{n} (b-a) ds$

であり、これを整理すると

$(-1)^{n}(b-a)^{m+n+1}\displaystyle \int_{0}^{1}s^{m}(1-s)^{n}ds$

すなわち

$(-1)^{n}(b-a)^{m+n+1}B(m \ , \ n)$

と、 $B(m \ , \ n)$ が登場します。

【解答】では

$x-a=t$
$t=(b-a)s$

という２段階の置換を、一つにまとめて

$x=t+a=(b-a)s+a$

と、一気にやってしまいます。

類題について

類題はこちら（画像をクリックするとPDFファイルで開きます。）

類題は $\displaystyle \frac{1}{6}$ 公式などの拡張がテーマであると一目でわかる問題です。

例題と並べて解くと、

$B(n \ , \ m)=\displaystyle \int_{0}^{1}x^{n}(1-x)^{m} dx$

との関連があることがおぼろげながらでも体感できると思います。

例題の解答はコチラ

類題の解答はコチラ

ウンチク

類題の(3) で示した等式の符号を微調整すると

$\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^{n}(x-\beta)^{m}=\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^{n}\{-(\beta-x)\}^{m} dx$

$=(-1)^{m}\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^{n}(\beta-x)^{m} dx$

であるため、

$\displaystyle \int_{\alpha}^{\beta}(x-\alpha)^{n}(\beta-x)^{m} dx=\displaystyle \frac{n!m!}{(n+m+1)!} (\beta-\alpha)^{n+m+1}$

とスッキリします。(この形をオイラーの第一種積分といいます。)

これに

$\alpha=0$ , $\beta=1$

を代入すると

$B(n \ , \ m)=\displaystyle \int_{0}^{1}x^{n}(1-x)^{m} dx$

を得るわけです。

一般的には

$B(p \ , \ q)=\displaystyle \int_{0}^{1}x^{p-1}(1-x)^{q-1} dx$

をベータ関数と呼びます。

ベータ関数はオイラーの第一種積分と同じ括りとなります。

これら $p$ , $q$ が自然数であれば、高校数学でも扱える範疇です。

ただ、本来は

$p$ , $q$ は実部が 0 より大きい複素数とする。