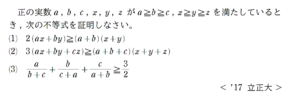例題はこちら(画像をクリックするとPDFファイルで開きます。)
類題はこちら(画像をクリックするとPDFファイルで開きます。)
チェビシェフの不等式と呼ばれる有名不等式を背景にもつ問題です。
例題の (1) , (2) の結果を拡張したものがチェビシェフの不等式で、入試においては本問のような具体例に対しての出題が目立ちます。
もちろん、テーマ性のある話題なので、うまく考える方法もありますが、試験場では愚直にゴリゴリ進めていってもたかが知れています。
例題はさらに欲張って (3) で 「Nesbitt (ネスビット) の不等式」と呼ばれる有名な(マニアックな)不等式まで盛り込んでいます。
(3) は差をとってゴリゴリするのはキツイものがあります。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 差をとってゴリゴリする路線はここでは割愛します。(【解1】を参照してください。) 以下、少し凝った路線を紹介します。 そのために、一つインストールしておきたい有名な不等式があります。 順列不等式 実数 \(a\) , \(b\) , \(c\) , \(x\) , \(y\) , \(z\) に対して、\(a \geq b \geq c\) , \(x \geq y \geq z\) が成り立っているとする。 今、\(x\) , \(y\) , \(z\) を並べ替えたものを \(p\) , \(q\) , \(r\) とし、 \((x \ , \ y \ , \ z)=(p \ , \ q \ , \ r)\) とする。 任意の順列に対応する\(p\) , \(q\) , \(r\) に対して \(ax+by+cz \geq ap+bq+cr \geq az+by+cx\) が成り立つ。 要するに 大きいもの同士をペアにすれば大きく、逆にすれば小さくなる ということです。 よくあるイメージ例として お金のわしづかみ が用いられます。 としてみましょう。 金額と枚数をペアにしてできる限りもらえる金額を多くしようと思ったらどうすればよいでしょうか。 もちろん、 というように、金額が大きいものを多くとりたくなるに決まっています。 この不等式は日本語名で正式名称があるわけではないらしいので、ここでは「順列不等式」と呼ばせていただきます。 (大学への数学では並べ替えの不等式などと呼ばれていますかね) 証明については確か入試問題でもあったと思いますので、また追記します。 順列不等式によれば $$\begin{eqnarray} で辺々加えると \(2(ay+bx) \leq (a+b)(x+y) \leq 2(ax+by)\) を得て、辺々 \(4\) で割ると \(\displaystyle \frac{ay+bx}{2} \leq \displaystyle \frac{a+b}{2}\cdot \displaystyle \frac{x+y}{2} \leq \displaystyle \frac{ax+by}{2}\) が得られます。 同様に $$\begin{eqnarray} で、辺々加えると \(3(az+by+cx) \leq (a+b+c) (x+y+z) \leq 3 (ax+by+cz)\) を得て、辺々 \(9\) で割ると \(\displaystyle \frac{az+by+cx}{3} \leq \displaystyle \frac{a+b+c}{3} \cdot \displaystyle \frac{x+y+z}{3} \leq \displaystyle \frac{ax+by+cz}{3}\) ということが言えます。 これを一般化すると チェビシェフの不等式 \(a_{1} \geq a_{2} \geq \cdots \geq a_{n}\) , \(b_{1} \geq b_{2} \geq \cdots \geq b_{n}\) のとき \(\displaystyle \frac{a_{n}b_{1}+\cdots+a_{1}b_{n}}{n} \leq \displaystyle \frac{a_{1}+\cdots+a_{n}}{n} \cdot \displaystyle \frac{b_{1}+\cdots+b_{n}}{n} \leq \displaystyle \frac{a_{1}b_{1}+\cdots+a_{n}b_{n}}{n}\) ということが言えます。 この形で見ると、「平均」という意味付けがあるため頭に残りやすいでしょう。 証明は順列不等式を用いれば上と同じ要領で示せます。 (3) は Nesbitt の不等式 正の実数 \(a\) , \(b\) , \(c\) に対して \(\displaystyle \frac{a}{b+c}+\displaystyle \frac{b}{c+a}+\displaystyle \frac{c}{a+b} \leq \displaystyle \frac{3}{2}\) が成り立つ という有名な不等式まんまです。 ノーヒントだと結構ツライものがあるかもしれませんが、幸いにも本問では誘導となるチェビシェフ不等式があります。 (2) の \(x\) , \(y\) , \(z\) に何をぶち込みたいかを考えてみてください。 なお、チェビシェフの不等式が決め手となるのであれば、チェビシェフの不等式の決め手となる順列不等式を用いても、解けるはずです。 誘導に沿った解法は【解 1】、順列不等式を用いたものは【解 2】としてあります。 ただ、順列不等式を証明なしで認めてよいかについては何とも言えません。 よく観察してみると、チェビシェフの不等式の応用だということが分かるでしょうか。 もちろん、誰にも文句を言わせないぞという態度で解くのであれば、普通に差をとる路線ですし、この程度であれば腕力で押し切れますので、チェビシェフの不等式路線はあくまで観賞用の解答でしょう。例題について
例題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)
順列不等式
チェビシェフの不等式
\left\{
\begin{array}{l}
ay+bx \leq ax+by \leq ax+by \\
ay+bx \leq ay+bx \leq ax+by
\end{array}
\right.
\end{eqnarray}$$
\left\{
\begin{array}{l}
az+by+cx \leq ax+bz+cy \leq ax+by+cz \\
az+by+cx \leq az+by+cx \leq ax+by+cz \\
az+by+cx \leq ay+bx+cz \leq ax+by+cz
\end{array}
\right.
\end{eqnarray}$$Nesbitt ( ネスビット ) の不等式について
類題について
類題はこちら(再掲)(画像をクリックするとPDFファイルで開きます。)