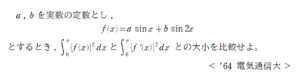例題はこちら（画像をクリックするとPDFファイルで開きます。）
ウィルティンガーの不等式と呼ばれる
ウィルティンガーの不等式
\(f(x)\) が周期 \(2\pi\) をもち、\(\displaystyle \int_{0}^{2\pi} f(x) dx=0\) を満たすならば
\(\displaystyle \int_{0}^{2\pi} \{f'(x)\}^{2} dx \geq \displaystyle \int_{0}^{2\pi} \{f(x)\}^{2} dx\)
が成り立つ。
という、解析学でしばしば現れる不等式をネタにした問題です。
入試的には、三角関数や、積分計算における基本的な運用能力を見る問題という位置づけとなるでしょう。
この不等式自体は知らなくても、確かな力があれば素直に解き進めていけば手なりに解決しますので、特に心配することはありません。
経験という意味からすると、途中においては三角関数の直交性に関する経験が定着していると、若干見通しがよくなります。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む 今回登場する \(\{f'(x)\}^{2}\) , \(\{f(x)\}^{2}\) は具体的には です。 したがって \(\displaystyle \int_{0}^{2\pi} \{f'(x)\}^{2} dx\) , \(\displaystyle \int_{0}^{2\pi} \{f(x)\}^{2} dx\) を計算するにあたって要となるのは という定積分です。 \(\displaystyle \int_{0}^{2\pi} \{f'(x)\}^{2} dx\) , \(\displaystyle \int_{0}^{2\pi} \{f(x)\}^{2} dx\) を計算するにあたり、多少文字の入れ替わりなどはありますが、本質的にこの３つが肝ということになります。 \(\displaystyle \int_{0}^{2\pi} \cos^{2}{mx} dx\) , \(\displaystyle \int_{0}^{2\pi} \sin^{2}{nx} dx\) については 半角公式による次数下げ \(\displaystyle \int_{0}^{2\pi} \cos{mx}\sin{nx} dx\) については 積和公式 により仕留めることは、悩むことなく捌きたいところです。 積分は基本的に和の形と相性が良いため、三角関数における積和公式は、積を和の形に直すためのうってつけのツールです。 三角関数の直交性に関する経験が定着していると、 \(\displaystyle \int_{0}^{2\pi} \cos{mx}\sin{nx} dx=0\) と、\(0\) になることが見えるため、心理的には楽かもしれません。 途中現れる場合分けには気を付けましょう。 (1) ができれば \(\displaystyle \int_{0}^{2\pi}\{f'(x)\}^{2} dx-\displaystyle \int_{0}^{2\pi}\{f(x)\}^{2} dx=\pi\{p^{2}(m^{2}-1)+q^{2}(n^{2}-1)\}\) という関係式が得られているはずです。 この値が \(0\) となるとき、すなわち \(p^{2}(m^{2}-1)+q^{2}(n^{2}-1)=0\) となるときを考えるわけです。 これは、\(m\) , \(n\) が正の整数ということを考えると \(0\) 以上の実数\(+\)\(0\) 以上の実数 という構造をしています。 したがって、各々が \(0\) となる $$\begin{eqnarray} となるときを考えることになります。 例題よりさらに具体的になっており、このあたりの三角関数や積分に関する基礎を確認する手ごろな問題でしょう。(1) について
(2) について
\left\{
\begin{array}{l}
p^{2}(m^{2}-1)=0\\
q^{2}(n^{2}-1)=0
\end{array}
\right.
\end{eqnarray}$$類題について
類題はこちら（画像をクリックするとPDFファイルで開きます。）
