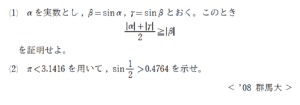問題はこちら(画像をクリックするとPDFファイルで開きます。)
\(\sin{\displaystyle \frac{1}{2}}\) に関する数値評価の問題です。
(1) という誘導があるため、その誘導を利用すれば (2) の数値評価自体はそこまでひっかかることはないと思います。
厄介なのは (1) で、周期性を持つ \(\sin{x}\) の扱い、及び絶対値の処理をどのように処理するかという構想力が問われます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 結局 \(|\alpha|+|\gamma|-2|\beta| \geq 0\) という不等式を示せばよいことになります。 \(|\alpha|+|\gamma|-2|\beta|\) を「小さくしよう、小さくしよう」という気持ちで評価してみます。 その気持ちで \(|\gamma|\) をカットして小さくすると \(|\alpha|+|\gamma|-2|\beta| \geq |\alpha|-2|\beta|\) ということになります。 ここで、\(|\beta|=|\sin{\alpha}| \leq 1\) です。 なので、\(|\alpha| \geq 2\) であれば \(|\alpha|-2|\beta| \geq 0\) となり、\(|\alpha|+|\gamma|-2|\beta| \geq 0\) が成立します。 そうなると、\(|\alpha| \lt 2\) のときはどうなんだ?ということになり、その場合をつぶす方向になります。 絶対値を含む処理を考えると という場合分けを考えつきたいところです。 \(\sin{\alpha} \geq 0\) ですから、 \(\beta \geq 0\) \(0 \leq \beta=\sin{\alpha} \leq1\) ですから、 \(\gamma \geq 0\) これより \(|\alpha|+|\gamma|-2|\beta|=\alpha+\gamma-2\beta\) と絶対値は外れます。 そうなると \(\alpha+\gamma-2\beta=(\alpha-\beta)-(\beta-\gamma)\) すなわち、 \((\alpha-\sin{\alpha})-(\beta-\sin{\beta})\) と見たくなります。 そうなってくると、\(f(x)=x-\sin{x}\) などと関数を設定し、\(f(\alpha)\) と \(f(\beta)\) の大小を比較する方針が思いつきます。 \(y=x\) , \(y=\sin{x}\) が奇関数であることを考えると \(\alpha=-\alpha'\) とおくと、\(0 \lt \alpha' \lt 2\) ですから、上述の場合に帰着し、そこから一気に話が進みます。 今回の \(\alpha\) , \(\beta\) , \(\gamma\) は合成写像的に定まっていきますから、それを視覚化していく路線も考えられます。 ただ、\(\alpha\) が一般の実数であるため、少しウルサイことになります。 この路線については【戦略2】【解2】で触れてあります。 (1) で示した \(\displaystyle \frac{|\alpha|+|\sin{\sin{\alpha}}|}{2} \geq |\sin{\alpha}|\) に対して、\(\sin{\displaystyle \frac{1}{2}}\) を登場させようと思ったら \(\alpha=\displaystyle \frac{\pi}{6}\) を代入したくなると思います。 後は手なりに進んでいきます。 炎上を覚悟でノーヒントでこの手の問題を出題する大学は少ないと思いますが、ノーヒントで出題されたときを想定しておきます。 知識に頼ることにはなりますが、\(\sin{x}\) を \(x\) の整式で近似するテイラー展開(マクローリン展開) \(\sin{x}=\displaystyle \frac{x}{1!}-\displaystyle \frac{x^{3}}{3!}+\displaystyle \frac{x^{5}}{5!}-\displaystyle \frac{x^{7}}{7!}+\cdots\) を基にした不等式 を利用することが考えられます。 証明は差を取って微分してゴリゴリすれば証明できます。 この不等式に \(x=\displaystyle \frac{1}{2}\) を代入すれば \(\sin{\displaystyle \frac{1}{2}} \geq \displaystyle \frac{23}{48}=0.4791\cdots\) を得ることができます。 等式を繋ぐのではなく、不等式を繋いでいく評価の話題は苦手意識をもつ人も多いと思います。 場数を踏むとともに、発想の種となるような考え方や見方を自分のものにしていく必要があります。 数値評価については以下のシリーズ 数値評価 第1講【円周率πの評価】【2019年度 埼玉大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 「数値評価」というテーマを扱います。 このシリーズの一覧はこちら 今回は円周率 \(\pi\) の評価です。 第1回ということもあり、まずは丁寧な誘導のついた問題をもってきました。 (1)は展開して定積分を計算するだけです。 (2)は \(x=\tan\theta\) \((-\displaystyle\frac{\pi}{2} \lt \theta \lt \displaystyle\frac ... 数値評価 第2講【ネイピア数eの評価】【2010年度 横浜市立大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 「数値評価」シリーズの第2弾です。 このシリーズの一覧はこちら 前回の第1弾は円周率 \(\pi\) の評価でした。 今回はネイピア数 \(e\) の評価です。 案の定ヒントめいた不等式が誘導としてついています。 前回と違い、今回はちょっとだけオチで一工夫が必要です。 (2) の不等式に \(a=1\) をそのまま代入してもうまくいきません。 今回の問題を通じて教訓として学んでほしいことは 評価に失敗したときのリカ ... 問題はこちら(画像をクリックするとPDFファイルで開きます。) 「数値評価」シリーズの第3弾です。 このシリーズの一覧はこちら 今回は \(e^{\pi}\) の評価です。 前回までと違い、今回はノーヒントでの出題です。 まず、今回の定積分 \(\displaystyle \int_{0}^{\pi} e^{x}\sin^{2} x dx\) は計算可能です。 次数を下げるために半角公式でほぐした後は ポイント 【 \(\displaystyle \int_ ... 数値評価 第4講【e^eの評価】【1992年度 北海道大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 「数値評価」シリーズの第4弾です。 このシリーズの一覧はこちら 今回は \(e^e\) の評価です。 ノーヒントでの出題であるため、基本的な構想を自分で組み立てる必要があります。 与えられた近似値を単純に使うとなると、手計算できる範囲では $$e^2 \lt e^e \lt e^3$$ とやるのが普通でしょうか。 これを計算しても、 $$7.387524 \lt e^e \lt 20.0792902 ... 数値評価 第5講【log2の評価】【2007年度 東京大学】 問題はこちら(画像をクリックするとPDFファイルで開きます。) 「数値評価」シリーズの第5弾です。 このシリーズの一覧はこちら 今回は \(\log{2}\) という自然対数の評価です。 (1) という誘導設問がありますが、単純に使うと失敗します。 恐らくほとんどの人が最初失敗して、そこからリカバリーしきれるかどうかという勝負になるでしょう。 不等式の精度を高めるために(誤差を小さくするために)どのようにすべきか、という部分に脳みそをつかっていきたいところです。 (以下ネタバレ注意) + ク ... でもじっくり扱っていますので、場数を踏みたい方はぜひどうぞ。(1) について
小さくしようと評価する路線
\(0 \leq \alpha \lt 2\)のとき
\(-2 \lt \alpha \lt 0\) のとき
視覚化する路線
(2) について
ノーヒントだと