問題はこちら(画像をクリックするとPDFファイルで開きます。)
\(1^{k}\) から \(n^{k}\) までの \(k\) 乗数の相加平均に関する不等式証明の問題です。
見慣れない記号に圧倒されるかもしれませんが、紐解いていけば、これまでの学習が活かせるような形が現れるはずで、それを見落とさずに捌いていきましょう。
とは言え、最後まで完答するためには
機械的なマニュアルではない、観察力
を要する部分もあるため、試験場で確保できると破壊力がある難易度です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む ひとまず、今回与えられている \(M(n \ , \ k)\) という記号を書き下していきます。 \(M(n \ , \ k)\) は \(1^{k}\) , \(2^{k}\) , \(\cdots\) , \(n^{k}\) という \(n\) 個の数の相加平均なので \(M(n \ , \ k)=\displaystyle \frac{1^{k}+2^{k}+\cdots+n^{k}}{n}\) ということになります。 したがって、今回証明したい不等式の真ん中の項に現れる \(\displaystyle \frac {M(n \ , \ k)}{n^{k}}\) というのは $$\begin{eqnarray} という形となり、区分求積法、及びそれにまつわる「面積の総和」を彷彿とさせる形が現れます あるいは 重要
求められない \(\displaystyle \sum_{ \ }^{ \ }\) は面積評価 という格言からインスピレーションしてもよいでしょう。 いずれにせよ、\(y=x^{k}\) のグラフを用いて面積評価をすることを考えていきます。 面積評価ということを想起すると、示すべき不等式の真ん中にある \(\displaystyle \frac {1}{k+1}\) というのは \(\displaystyle \frac {1}{k+1}=\displaystyle \int_{0}^{1} x^{k} dx\) というように見えてくるはずです。 このことから 長方形の面積の総和 \(\displaystyle \frac {1}{n}(\displaystyle \frac {1^{k}}{n^{k}}+\displaystyle \frac {2^{k}}{n^{k}}+\cdots+\displaystyle \frac {n^{k}}{n^{k}})\) を \(S\) とすると \(\displaystyle \frac {1}{n}(\displaystyle \frac {1^{k}}{n^{k}}+\displaystyle \frac {2^{k}}{n^{k}}+\cdots+\displaystyle \frac {n^{k}}{n^{k}})-\displaystyle \frac {1}{k+1}\) というのは \(S-\displaystyle \int_{0}^{1} x^{k} dx\) ということになり、これを \(T\) とすると、\(T\) は という図における打点部分の面積の総和ということになります。 この \(T\) を今回上からと下からで押さえることになります。 示すべき不等式の一つとして \(T \leq \displaystyle \frac{1}{n}\) があります。 先ほど、\(T\) のもつ図形的な意味を見出したわけですから、右辺の \(\displaystyle \frac {1}{n}\) にも図形的な意味合いを持たせたくなると思います。 そうなると \(\displaystyle \frac {1}{n}\) は上の図において 長方形 \(\mathrm{ABCD}\) の面積 ということを看破したいところです。 はみ出ている角っこの総和 \(T\) と長方形 \(\mathrm{ABCD}\) の面積を比較するわけですが、バラバラのままだと比較しづらいと思います。 そこで、上の図のように、 という工夫をしてやります。 これにより、 \(T \leq \displaystyle \frac{1}{n}\) ということが言えます。 今度は \(\displaystyle \frac{1}{2n} \leq T\) と、\(T\) を下から評価するのが目標です。 \(\displaystyle \frac{1}{2n}\) に図形的な意味を持たせようと思うと、 \(\triangle{\mathrm{ABC}}\) の面積 などということになるでしょうか。 ただ、これだと目に見えて明らかというわけではないでしょう。 ここからが頭を使う部分です。 というか、モノの見え方の問題です。 パッと見えると気持ちよいと思います。 ぜひ、答えを見る前に一考してみましょう。見慣れない記号を書き下す
\displaystyle \frac {M(n \ , \ k)}{n^{k}} &=& \displaystyle \frac {1}{n^{k}} \cdot \displaystyle \frac {1^{k}+2^{k}+\cdots+n^{k}}{n}\\
&=& \displaystyle \frac {1}{n}(\displaystyle \frac {1^{k}}{n^{k}}+\displaystyle \frac {2^{k}}{n^{k}}+\cdots+\displaystyle \frac {n^{k}}{n^{k}})
\end{eqnarray}$$グラフ的なイメージ
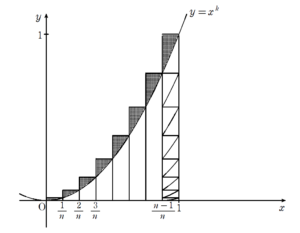
上からの評価
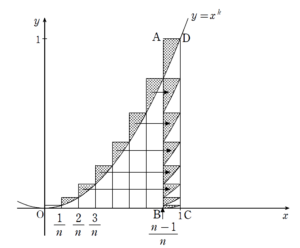
下からの評価

